题目内容
11.计算与化简(1)($\frac{1}{2}$)-2+|2-$\sqrt{12}$|-2$\sqrt{3}$+(π-3.14)0
(2)$\frac{{a}^{2}}{a+3}$÷$\frac{6a}{{a}^{2}-9}$.
分析 (1)本题涉及负整数指数幂、零指数幂、绝对值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)将除法变为乘法,再因式分解约分计算即可求解.
解答 解:(1)($\frac{1}{2}$)-2+|2-$\sqrt{12}$|-2$\sqrt{3}$+(π-3.14)0
=4+2$\sqrt{3}$-2-2$\sqrt{3}$+1
=3;
(2)$\frac{{a}^{2}}{a+3}$÷$\frac{6a}{{a}^{2}-9}$
=$\frac{{a}^{2}}{a+3}$×$\frac{(a+3)(a-3)}{6a}$
=$\frac{a(a-3)}{6}$.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、绝对值、二次根式等考点的运算.同时考查了分式的乘除法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )
如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )
 如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )
如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
6.设n为整数,且n<$\sqrt{40}$<n+1,则n的值为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
3.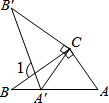 如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )
如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )
 如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )
如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )| A. | 110° | B. | 102° | C. | 105° | D. | 125° |
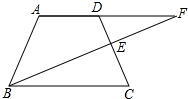 如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.
如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.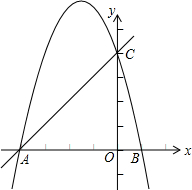 如图,抛物线y=ax2-bx-4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).
如图,抛物线y=ax2-bx-4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).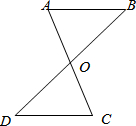 如图,已知AC与BD相交于点O,AO=CO,BO=DO,则AB=CD,请说明理由.
如图,已知AC与BD相交于点O,AO=CO,BO=DO,则AB=CD,请说明理由.