题目内容
13.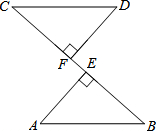 如图,DF=AE,AE⊥BC,DF⊥BC,CE=BF.求证:AB=CD.
如图,DF=AE,AE⊥BC,DF⊥BC,CE=BF.求证:AB=CD.
分析 由AE⊥BC,DF⊥BC,得∠DFC=∠AEB=90°,又由CE=BF,可得CE-EF=BF-EF,即CF=BE,所以,△DFC≌△AEB,即可得出.
解答 证明:∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
∵CE=BF,
∴CE-EF=BF-EF,即CF=BE,
∵DF=AE,
在RT△ABE与RT△DCF中,$\left\{\begin{array}{l}{CF=BE}\\{∠CFD=∠AEB}\\{DF=AE}\end{array}\right.$,
∴RT△ABE≌RT△DCF(SAS),
∴AB=CD.
点评 本题主要考查了全等三角形的判定与性质,在两直角三角形中,当斜边和一条直角边对应相等时,两直角三角形全等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列运算正确的是( )
| A. | 3-1=-3 | B. | $\sqrt{9}$=±3 | C. | (22)3=64 | D. | 56÷53=25 |
18.已知点A(-2,y1)、B(1,y2)、C(4,y3)都在函数y=x2-4x-5的图象上,则比较y1、y2、y3的大小正确的是( )
| A. | y2<y3<y1 | B. | y3<y1<y2 | C. | y1<y3<y2 | D. | y2<y1<y3 |
3.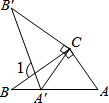 如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )
如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )
 如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )
如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )| A. | 110° | B. | 102° | C. | 105° | D. | 125° |
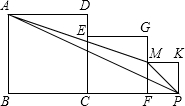 如图所示,三个正方形边长分别为1,2,3,求三角形AMP的面积.
如图所示,三个正方形边长分别为1,2,3,求三角形AMP的面积.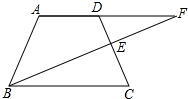 如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.
如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.