题目内容
10．
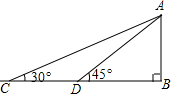如图，某校数学兴趣小组为测得校园里旗杆AB的高度，在操场的平地上选择一点C，测得旗杆顶端A的仰角为30°，再向旗杆的方向前进16米，到达点D处（C、D、B三点在同一直线上），又测得旗杆顶端A的仰角为45°，请计算旗杆AB的高度（结果保留根号）
分析 根据题意可以得到BD的长度，从而可以求得AB的高度．
解答 解：由题意可得，
CD=16米，
∵AB=CB•tan30°，AB=BD•tan45°，
∴CB•tan30°=BD•tan45°，
∴（CD+DB）×$\frac{\sqrt{3}}{3}$=BD×1，
解得BD=8$\sqrt{3}+8$，
∴AB=BD•tan45°=（$8\sqrt{3}+8$）米，
即旗杆AB的高度是（$8\sqrt{3}+8$）米．
点评 本题考查解直角三角形的应用-仰角俯角问题，解题的关键是明确题意，找出所求问题需要的条件．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知A，B是反比例函数y=$\frac{k}{x}$（k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于t的函数图象大致为（ ）
18．
如图，直线a∥b，直线c与直线a，b相交，若∠1=56°，则∠2等于（ ）
如图，直线a∥b，直线c与直线a，b相交，若∠1=56°，则∠2等于（ ）| A． | 24° | B． | 34° | C． | 56° | D． | 124° |
15．在解方程$\frac{x-1}{3}+x=\frac{3x+1}{2}$时，方程两边同时乘以6，去分母后，正确的是（ ）
| A． | 2x-1+6x=3（3x+1） | B． | 2（x-1）+6x=3（3x+1） | C． | 2（x-1）+x=3（3x+1） | D． | （x-1）+x=3（x+1） |
19．
如图，在平面直角坐标系中，点A的坐标为（4，3），那么cosα的值是（ ）
如图，在平面直角坐标系中，点A的坐标为（4，3），那么cosα的值是（ ）| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |