题目内容
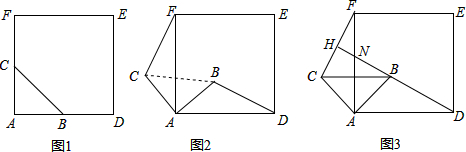
1.如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3$\sqrt{2}$时,求线段DH的长.
分析 (1)根据旋转变换的性质和全等三角形的判定定理证明△CAF≌△BAD,证明结论;
(2)①根据全等三角形的性质、垂直的定义证明即可;
②连接DF,延长AB交DF于M,根据题意和等腰直角三角形的性质求出DM、BM的长,根据勾股定理求出BD的长,根据相似三角形的性质列出比例式,计算即可得到答案.
解答 解:(1)BD=CF.
理由如下:由题意得,∠CAF=∠BAD=θ,
在△CAF和△BAD中,
$\left\{\begin{array}{l}{CA=BA}\\{∠CAF=∠BAD}\\{FA=DA}\end{array}\right.$,
∴△CAF≌△BAD,
∴BD=CF;
(2)①由(1)得△CAF≌△BAD,
∴∠CFA=∠BDA,
∵∠FNH=∠DNA,∠DNA+∠NDA=90°,
∴∠CFA+∠FNH=90°,
∴∠FHN=90°,即BD⊥CF;
②连接DF,延长AB交DF于M,
∵四边形ADEF是正方形,AD=3$\sqrt{2}$,AB=2,
∴AM=DM=3,BM=AM-AB=1,
∵△ABC绕点A逆时针旋转45°,
∴∠BAD=45°,
∴AM⊥DF,
∴DB=$\sqrt{D{M}^{2}+B{M}^{2}}$=$\sqrt{10}$,
∵∠MAD=∠MDA=45°,
∴∠AMD=90°,又∠DHF=90°,∠MDB=∠HDF,
∴△DMB∽△DHF,
∴$\frac{DM}{DH}$=$\frac{DB}{DF}$,即$\frac{3}{DH}$=$\frac{\sqrt{10}}{6}$,
解得,DH=$\frac{9\sqrt{10}}{5}$.
点评 本题考查的是正方形的性质、等腰直角三角形的性质、旋转变换的性质以及相似三角形的判定和性质,掌握旋转角的定义和旋转变换的性质、正确作出辅助线是解题的关键.

 名校课堂系列答案
名校课堂系列答案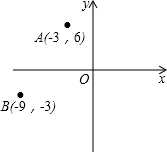 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )| A. | (-1,2) | B. | (-9,18) | C. | (-9,18)或(9,-18) | D. | (-1,2)或(1,-2) |
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
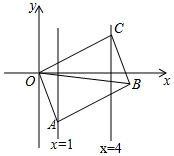 如图,已知?OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为5.
如图,已知?OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为5. 如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( )
如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( )
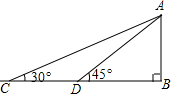 如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30°,再向旗杆的方向前进16米,到达点D处(C、D、B三点在同一直线上),又测得旗杆顶端A的仰角为45°,请计算旗杆AB的高度(结果保留根号)
如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30°,再向旗杆的方向前进16米,到达点D处(C、D、B三点在同一直线上),又测得旗杆顶端A的仰角为45°,请计算旗杆AB的高度(结果保留根号)