题目内容
2.先化简,再求值:$(\frac{1}{x}-\frac{1}{x+2})•\frac{{{x^2}-4}}{2}$,其中x=3.分析 首先通分计算括号里面的,再计算乘法,把多项式分解因式后约分,得出化简结果,再代入x的值计算即可.
解答 解:$(\frac{1}{x}-\frac{1}{x+2})•\frac{{{x^2}-4}}{2}$
=$\frac{2}{x(x+2)}$•$\frac{(x+2)(x-2)}{2}$
=$\frac{x-2}{x}$,
当x=3时,原式=$\frac{3-2}{3}$=$\frac{1}{3}$.
点评 此题考查了分式的化简求值,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时分式的分子分母出现多项式,应将多项式分解因式后再约分.

练习册系列答案
相关题目
7.近日,记者从潍坊市统计局获悉,2016年第一季度潍坊全市实现生产总值1256.77亿元,将1256.77亿用科学记数法可表示为(精确到百亿位)( )
| A. | 1.2×1011 | B. | 1.3×1011 | C. | 1.26×1011 | D. | 0.13×1012 |
17. 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )| A. | 22.5° | B. | 25° | C. | 23° | D. | 20° |
 如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( )
如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( )
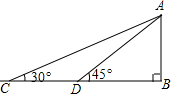 如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30°,再向旗杆的方向前进16米,到达点D处(C、D、B三点在同一直线上),又测得旗杆顶端A的仰角为45°,请计算旗杆AB的高度(结果保留根号)
如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30°,再向旗杆的方向前进16米,到达点D处(C、D、B三点在同一直线上),又测得旗杆顶端A的仰角为45°,请计算旗杆AB的高度(结果保留根号)