题目内容
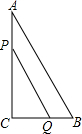 如图,在Rt△ACB中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动,它们的速度都是1米/秒,问:几秒后△PCQ的面积为Rt△ACB面积的一半?
如图,在Rt△ACB中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动,它们的速度都是1米/秒,问:几秒后△PCQ的面积为Rt△ACB面积的一半?考点:一元二次方程的应用
专题:几何动点问题
分析:根据题意∠C=90°,可以得出△ABC面积为
×6×8,△PCQ的面积为
(8-x)(6-x),设出t秒后满足要求,则根据△PCQ的面积是△ABC面积的一半列出等量关系求出t的值即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设经过x秒后△PCQ的面积是Rt△ACB面积的一半,
则:
=12,
解得x1=12(舍去),x2=2.
答:经2秒△PCQ的面积是Rt△ACB面积的一半.
则:
| (8-x)(6-x) |
| 2 |
解得x1=12(舍去),x2=2.
答:经2秒△PCQ的面积是Rt△ACB面积的一半.
点评:本题考查了三角形面积的计算方法,找到等量关系式,列出方程求解即可.要注意结合图形找到等量关系.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
为迎接普洱市茶叶节,有十五位同学参加茶文化知识竞赛,且他们的分数互不相同,取八位同学进入决赛,某人知道了自己的分数后,要能判断他能不能进入决赛,还需知道这十五位同学的分数的( )
| A、平均数 | B、众数 |
| C、最高分数 | D、中位数 |
若A=10a2+2b2-7a+6,B=a2+2b2+5a-1,则A-B的值是( )
| A、正数 | B、负数 | C、0 | D、可正可负 |
 如图在矩形ABCD中,AB=12,BC=16,E、F分别是AB、CD上的点,且AE=DF=8,两动点M、N都以2cm/s的速度分别从C、F两点沿CB、FE向B、E两点运动,判断当M、N运动多长时间能使矩形CFNM与矩形AEFD相似,并证明你的结论.
如图在矩形ABCD中,AB=12,BC=16,E、F分别是AB、CD上的点,且AE=DF=8,两动点M、N都以2cm/s的速度分别从C、F两点沿CB、FE向B、E两点运动,判断当M、N运动多长时间能使矩形CFNM与矩形AEFD相似,并证明你的结论. 如图,E为AC中点,点F在AB上,且
如图,E为AC中点,点F在AB上,且 一个上底和下底都是等边三角形的盒子,等边三角形的高为70cm,盒子的高为240cm,M为AB的中点,在M处有一只飞蛾要飞到E处,它的最短行程多少?
一个上底和下底都是等边三角形的盒子,等边三角形的高为70cm,盒子的高为240cm,M为AB的中点,在M处有一只飞蛾要飞到E处,它的最短行程多少? 如图,已知△ABC≌△DEC,B、C、D三点在同一直线上,∠B=60°,求∠1的度数.
如图,已知△ABC≌△DEC,B、C、D三点在同一直线上,∠B=60°,求∠1的度数.