题目内容
如图，E为AC中点，点F在AB上，且| AF |
| AB |
| 2 |
| 5 |
| EF |
| ED |
考点：相似三角形的判定与性质
专题：
分析：过F作FG∥BD，交AC于点G，则有
=
=
，又结合E为中点，找到CE与EG之间的关系，再结合△GFE∽△CDE，可求得比值．
| AF |
| AB |
| AG |
| AC |
| 2 |
| 5 |
解答：
解：过F作FG∥BD，交AC于点G，则有
=
=
，
又∵AE=EC，
∴AC=2CE，AG=AE-EG=CE-EG，
∴
=
，
整理可得
=
，
又∵FG∥BD，
∴△GFE∽△CDE，
∴
=
=
．
解：过F作FG∥BD，交AC于点G，则有| AF |
| AB |
| AG |
| AC |
| 2 |
| 5 |
又∵AE=EC，
∴AC=2CE，AG=AE-EG=CE-EG，
∴
| CE-EG |
| 2CE |
| 2 |
| 5 |
整理可得
| EG |
| EC |
| 1 |
| 5 |
又∵FG∥BD，
∴△GFE∽△CDE，
∴
| EF |
| ED |
| EG |
| EC |
| 1 |
| 5 |
点评：本题主要考查相似三角形的判定和性质的应用，解题的关键是通过作辅助线找到所求比值与已知比值之间的关系．
练习册系列答案
相关题目
-|-5|=（ ）
| A、5 | ||
B、-
| ||
| C、-5 | ||
D、
|
关于函数y=x+1，下列结论正确的是（ ）
| A、图象必经过点（-2，1） |
| B、y随x的增大减小 |
| C、当x＞-1时，y＜0 |
| D、图象经过第一、二、三象限 |
如图所示，锐角三角形ABC的两条高BD、CE相交于点O，且BE=CD．求证：点O在角BAC的角平分线上．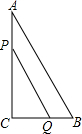
如图，在Rt△ACB中，∠C=90°，AC=8cm，BC=6cm，点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动，它们的速度都是1米/秒，问：几秒后△PCQ的面积为Rt△ACB面积的一半？
图（1）是图（2）正方体的表面展开图，请在图（2）的正方体中将线段BD、EF画出来．
如图，是由9个长和宽分别为2，1的长方形拼成的，任意连接这些小长方形的若干个顶点，可得到一些线段．试算出长度不是有理数的所有线段的平方的值．