Question

15．如图①，在△ABC中，AB=AC，BC=2a（单位：cm），sinB=$\frac{3}{5}$．动点P以1cm/s的速度从点B出发，沿折线B-A-C运动到点C时停止运动．设点P出发x（s）时，△PBC的面积为y（cm²）．已知y与x的函数图象如图②所示，请根据图中信息，解答下列问题：
（1）若a=4时，求图①中AB的长度；
（2）直接写出图②中D点的坐标（$\frac{5}{4}a$，$\frac{3}{4}$a²）；（用含a的代数式表示）
（3）当a为何值时，△ABC∽△DOE．

Answer 1

分析 （1）过点A作AM⊥BC于M，根据等腰三角形的性质得到BM=$\frac{1}{2}$BC=4，设AM=3x，AB=5x，根据勾股定理得到BM=$\sqrt{A{B}^{2}-A{M}^{2}}$=4x，即可得到结论；
（2）根据等腰三角形的性质得到BM=$\frac{1}{2}$BC=a，设AB=5x，AM=3x，得到BM=4x，求得AM=$\frac{3}{4}$a，AB=$\frac{5}{4}$a，根据三角形的面积公式于是得到结论；
（3）作DF⊥OE于F，根据题意得到DO=DE推出当且仅当∠DOE=∠ABC时，△DOE∽△ABC，根据三角函数的定义得到tan∠DOF=$\frac{3}{5}$a，tan∠B=$\frac{3}{4}$，得到方程，于是得到结果．

解答 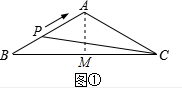解：（1）过点A作AM⊥BC于M，
∵AB=AC，BC=2acm=8cm，
∴BM=$\frac{1}{2}$BC=4，
∵sinB=$\frac{3}{5}$，
∴设AM=3x，AB=5x，
∴BM=$\sqrt{A{B}^{2}-A{M}^{2}}$=4x，
∴x=1，
∴AB=5，

（2）由题意得：∵AB=AC，BC=2acm，
∴BM=$\frac{1}{2}$BC=a，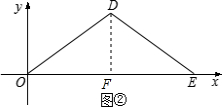
∵sinB=$\frac{3}{5}$，
设AB=5x，AM=3x，
∴BM=4x，
∴x=$\frac{a}{4}$，
∴AM=$\frac{3}{4}$a，AB=$\frac{5}{4}$a，
∴S_△ABC=$\frac{1}{2}$BC•AM=$\frac{1}{2}$×2a×$\frac{3}{4}$a=$\frac{3}{4}$a²，
∴D（ $\frac{5}{4}a$，$\frac{3}{4}$a²）；
故答案为：$\frac{5}{4}a$，$\frac{3}{4}$a²，

（3）作DF⊥OE于F，
∵AB=AC，点P以1cm/s的速度运动，
∴点P在边AB和AC上的运动时间相同，
∴点F是OE的中点，
∴DF是OE的垂直平分线，
∴DO=DE，∵AB=AC，
∴当且仅当∠DOE=∠ABC时，△DOE∽△ABC，
在Rt△DOF中，tan∠DOF=$\frac{DF}{OF}$=$\frac{\frac{3}{4}{a}^{2}}{\frac{5}{4}a}$=$\frac{3}{5}$a，
∵tan∠B=$\frac{AM}{BM}$=$\frac{\frac{3}{4}a}{a}$=$\frac{3}{4}$，
∴$\frac{3}{5}$a=$\frac{3}{4}$，
∴a=$\frac{5}{4}$，
当a=$\frac{5}{4}$时，△DOE∽△ABC．

点评 此题考查了相似三角形的判定与性质，等腰三角形的判定与性质以及线段垂直平分线的性质等知识．此题综合性较强，解题的关键是方程思想与数形结合思想的应用．