题目内容
6.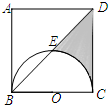 如图,正方形ABCD边长为2,以BC为直径的半圆O交对角线BD于E,则阴影部分面积为(结果保留π)$\frac{3}{2}$-$\frac{π}{4}$.
如图,正方形ABCD边长为2,以BC为直径的半圆O交对角线BD于E,则阴影部分面积为(结果保留π)$\frac{3}{2}$-$\frac{π}{4}$.
分析 首先连接OE,然后求出EO长,再计算出S梯形CDEO和S扇形COE,再求差即可得到阴影部分的面积.
解答 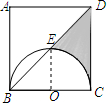 解:连接OE,
解:连接OE,
∵四边形ABCD是正方形,
∴∠CBD=45°,
∵正方形ABCD边长为2,
∴OB=OE=1,
∴∠BOE=90°,
∴S阴=S梯形CDEO-S扇形COE=$\frac{1}{2}$×(1+2)×1-$\frac{90}{360}$π×12=$\frac{3}{2}$-$\frac{π}{4}$.
故答案为:$\frac{3}{2}$-$\frac{π}{4}$.
点评 此题主要考查了扇形的面积计算,关键是掌握扇形面积计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=$\frac{nπ{R}^{2}}{360}$.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
11.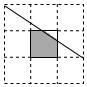 如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
 如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )| A. | $\frac{5}{6}$ | B. | $\frac{7}{8}$ | C. | $\frac{9}{10}$ | D. | $\frac{11}{12}$ |
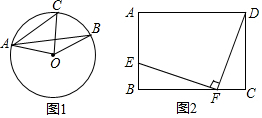
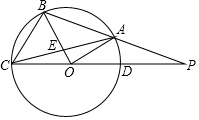 如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点.
如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点.