题目内容
14.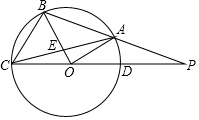 如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点.
如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点.(1)判断A是否是PB的中点,并说明理由;
(2)若⊙O半径为8,试求BC的长.
分析 (1)连接AD,由CD是⊙O的直径,得到AD⊥AC,推出AD∥OB,根据平行线等分线段定理得到PA=AB;
(2)根据相似三角形的性质得到OB=8,求得AD=4,根据勾股定理得到AC=$\sqrt{C{D}^{2}-A{D}^{2}}$=4$\sqrt{15}$,根据垂径定理得到AE=CE=2$\sqrt{15}$,由勾股定理即可得到结论
解答 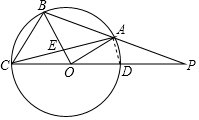 解:(1)A是PB的中点,
解:(1)A是PB的中点,
理由:连接AD,
∵CD是⊙O的直径,
∴AD⊥AC,
∵OB⊥AC,
∴AD∥OB,
∵PD=OD,
∴PA=AB,
∴A是PB的中点;
(2)∵AD∥OB,
∴△APD∽△BPO,
∴$\frac{AD}{OB}=\frac{PD}{OP}=\frac{1}{2}$,
∵⊙O半径为8,
∴OB=8,
∴AD=4,
∴AC=$\sqrt{C{D}^{2}-A{D}^{2}}$=4$\sqrt{15}$,
∵OB⊥AC,
∴AE=CE=2$\sqrt{15}$,
∵OE=$\frac{1}{2}$AD=2,
∴BE=6,
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=4$\sqrt{6}$.
点评 本题考查了垂径定理,勾股定理,圆周角定理,平行线的判定,相似三角形的判定和性质,正确的识别图形是解题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
16.在-2,$\frac{1}{2}$,-3,6四个数中,最小的数是( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | -3 | D. | 6 |
9.抛物线C1:y1=a1x2+b1x+c1中,函数值y1与自变量x之间的部分对应关系如下表:
(1)设抛物线C1的顶点为P,则点P的坐标为(-1,0);
(2)现将抛物线C1沿x轴翻折,得到抛物线C2:y2=a2x2+b2x+c2,试求C2的解析式;
(3)现将抛物线C2向下平移,设抛物线在平移过程中,顶点为点D,与x轴的两交点为点A、B.
①在最初的状态下,至少向下平移多少个单位,点A、B之间的距离不小于6个单位?
②在最初的状态下,若向下平移m(m>0)个单位时,对应的线段AB长为n,请直接写出m与n的等量关系.
| x | … | -3 | -2 | -1 | 1 | 3 | 4 | … |
| y1 | … | -4 | -1 | 0 | -4 | -16 | -25 | … |
(2)现将抛物线C1沿x轴翻折,得到抛物线C2:y2=a2x2+b2x+c2,试求C2的解析式;
(3)现将抛物线C2向下平移,设抛物线在平移过程中,顶点为点D,与x轴的两交点为点A、B.
①在最初的状态下,至少向下平移多少个单位,点A、B之间的距离不小于6个单位?
②在最初的状态下,若向下平移m(m>0)个单位时,对应的线段AB长为n,请直接写出m与n的等量关系.
19.下列算式中,结果等于x6的是( )
| A. | x2•x2•x2 | B. | x2+x2+x2 | C. | x2•x3 | D. | x4+x2 |
3.下列结论错误的是( )
| A. | 平行四边形既是中心对称又是轴对称图形 | |
| B. | 矩形的四个角相等 | |
| C. | 正方形的对角线互相垂直平分且相等 | |
| D. | 菱形的四条边相等 |
4.下列各数中,相反数为4的是( )
| A. | 4 | B. | -4 | C. | 0.4 | D. | 0.25 |
 飞行员在空中观察地面的区域是一个圆(如图),当观察角α为50°,飞机的飞行高度h为9.8×102m时,观察区域的半径为多少米(结果精确到1m)?如果观察角度不变,要使观察区域面积增加1倍,那么飞机要升高多少米(精确到1m)?
飞行员在空中观察地面的区域是一个圆(如图),当观察角α为50°,飞机的飞行高度h为9.8×102m时,观察区域的半径为多少米(结果精确到1m)?如果观察角度不变,要使观察区域面积增加1倍,那么飞机要升高多少米(精确到1m)?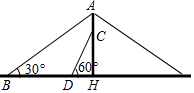 芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732)
芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732)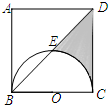 如图,正方形ABCD边长为2,以BC为直径的半圆O交对角线BD于E,则阴影部分面积为(结果保留π)$\frac{3}{2}$-$\frac{π}{4}$.
如图,正方形ABCD边长为2,以BC为直径的半圆O交对角线BD于E,则阴影部分面积为(结果保留π)$\frac{3}{2}$-$\frac{π}{4}$.