题目内容
 如图:在四边形ABCD中,∠ABC=90°,AB=3
如图:在四边形ABCD中,∠ABC=90°,AB=3| 2 |
| 7 |
①四边形ABCD的面积.
②求Rt△ABC中斜边AC边上的高BE.
考点:勾股定理
专题:
分析:①根据勾股定理求得AC=5;由勾股定理的逆定理判定△ACD为直角三角形,则四边形ABCD的面积=△ABC的面积+△ACD的面积;
②根据三角形的面积公式即可得到Rt△ABC中斜边AC边上的高BE.
②根据三角形的面积公式即可得到Rt△ABC中斜边AC边上的高BE.
解答:解:①如图,∵在△ABC中,∠ABC=90°,AB=3
,BC=
,
∴由勾股定理得 AC2=AB2+BC2=25.则AC=5,
又∵在△ACD中,BC=12,AD=13,
∴AD2=CD2+AC2=169,
∴△ACD为直角三角形,且∠ACD=90°,
∴S四边形ABCD=S△ABC+S△ACD=
AB•BC+
AC•CD=
×3
×
+
×5×12=
+30.
即四边形ABCD的面积是
+30.
②∵
AC•BE=
AB•BC,
∴
×5BE=
×3
×
,
解得BE=
.
故Rt△ABC中斜边AC边上的高BE为
.
| 2 |
| 7 |
∴由勾股定理得 AC2=AB2+BC2=25.则AC=5,
又∵在△ACD中,BC=12,AD=13,
∴AD2=CD2+AC2=169,
∴△ACD为直角三角形,且∠ACD=90°,
∴S四边形ABCD=S△ABC+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 7 |
| 1 |
| 2 |
3
| ||
| 2 |
即四边形ABCD的面积是
3
| ||
| 2 |
②∵
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 7 |
解得BE=
3
| ||
| 5 |
故Rt△ABC中斜边AC边上的高BE为
3
| ||
| 5 |
点评:本题考查了勾股定理,勾股定理的逆定理,以及三角形的面积.此题属于易错题,同学们往往忽略了推知△ACD为直角三角形.

练习册系列答案
相关题目
 如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE. 如图,在?ABCD中,点E、F分别在AD、BC上,且AE=CF.
如图,在?ABCD中,点E、F分别在AD、BC上,且AE=CF. 如图,已知:DF∥AC,∠C=∠D.
如图,已知:DF∥AC,∠C=∠D. 如图,在△ABC中,D为BC上一点,DE∥AC交AB于E点,DF∥AB交AC于F点,当AD满足条件
如图,在△ABC中,D为BC上一点,DE∥AC交AB于E点,DF∥AB交AC于F点,当AD满足条件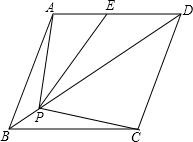 菱形ABCD的边长为2,∠ABC=60°,E是AD边中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是
菱形ABCD的边长为2,∠ABC=60°,E是AD边中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是