题目内容
如图，在?ABCD中，点E、F分别在AD、BC上，且AE=CF．求证：四边形BFDE是平行四边形．
考点：平行四边形的判定与性质
专题：证明题
分析：由四边形ABCD是平行四边形，根据平行四边形对边平行且相等，即可得AD∥BC，AD=BC，又由AE=CF，即可证得DE=BF，然后根据对边平行且相等的四边形是平行四边形，即可证得四边形BFDE是平行四边形．
解答：证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵AE=CF，
∴AD-AE=BC-CF，
∴ED=BF，
又∵AD∥BC，
∴四边形BFDE是平行四边形．
∴AD∥BC，AD=BC，
∵AE=CF，
∴AD-AE=BC-CF，
∴ED=BF，
又∵AD∥BC，
∴四边形BFDE是平行四边形．
点评：此题考查了平行四边形的性质与判定，注意熟练掌握定理与性质是解决问题的关键．
练习册系列答案
相关题目
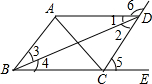如图，∠5=∠CDA=∠ABC，∠1=∠4，∠2=∠3，∠BAD+∠CDA=180°，填空：
如图：在四边形ABCD中，∠ABC=90°，AB=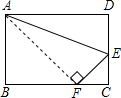
如图，折叠矩形，使点D落在BC边上的点F处，BC=10cm，AB=8cm，则FC=