题目内容
16. 如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD为54°.
如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD为54°.
分析 根据等腰三角形的性质由已知可求得∠A的度数,再根据垂直的定义和三角形内角和定理不难求得∠ABD的度数.
解答 解:∵AB=AC,∠ABC=72°,
∴∠ABC=∠ACB=72°,
∴∠A=36°,
∵BD⊥AC,
∴∠ABD=90°-36°=54°.
故答案为54°.
点评 本题主要考查等腰三角形的性质,解答本题的关键是会综合运用等腰三角形的性质和三角形的内角和定理进行答题,此题难度一般.

练习册系列答案
相关题目
11.点P的坐标为(3a-2,8-2a),若点P到两坐标轴的距离相等,则a的值是( )
| A. | $\frac{2}{3}$或4 | B. | -2或6 | C. | -$\frac{2}{3}$或-4 | D. | 2或-6 |
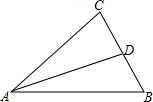 如图所示,已知AD是△ABC的中线.
如图所示,已知AD是△ABC的中线.