题目内容
7. 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a-b+c<0;⑤3a+c>0.其中正确结论的序号是①④⑤.
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a-b+c<0;⑤3a+c>0.其中正确结论的序号是①④⑤.
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴x=-1计算2a+b与0的关系;再由根的判别式与根的关系,进而对所得结论进行判断.
解答 解:∵图象和x轴有两个交点,
∴b2-4ac>0,
∴b2>4ac,∴①正确;
∵从图象可知:a>0,c<0,-$\frac{b}{2a}$=-1,b=2a>0,
∴abc<0,∴②错误;
∵b=2a>0
∴2a+b=4a>0,∴③错误;
∵x=-1时,y<0,
∴a-b+c<0,∴④正确;
∵x=1时,y>0,
∴a+b+c>0,
把b=2a代入得:3a+c>0,选项⑤正确;
故答案为①④⑤.
点评 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
2.若2b2nam与-5ab6的和仍是一个单项式,则m、n值分别为( )
| A. | 6,$\frac{1}{2}$ | B. | 1,2 | C. | 1,3 | D. | 2,3 |
12.下列说法正确的是( )
| A. | 1-x是一次单项式 | B. | 单项式a的系数和次数都是1 | ||
| C. | 2m-(2m+n)的运算结果为4m-n | D. | 单项式2×104x2的系数是2 |
16.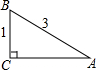 坡比常用来反映斜坡的倾斜程度,如图所示,斜坡AB的坡比为( )
坡比常用来反映斜坡的倾斜程度,如图所示,斜坡AB的坡比为( )
 坡比常用来反映斜坡的倾斜程度,如图所示,斜坡AB的坡比为( )
坡比常用来反映斜坡的倾斜程度,如图所示,斜坡AB的坡比为( )| A. | 1:2$\sqrt{2}$ | B. | 2$\sqrt{2}$:1 | C. | 1:3 | D. | 3:1 |
17.下列方程中,关于x的一元二次方程是( )
| A. | x2+x+y=0 | B. | $\frac{1}{2}$x2-3x+1=0 | C. | (x+3)2=x3+2x | D. | x2+$\frac{1}{x}$=2 |
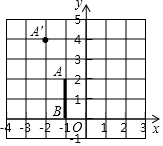 如图,在平面直角坐标系xOy中,以原点为位似中心,线段AB与线段A′B′是位似图形,若A(-1,2),B(-1,0),A′(-2,4),则B′的坐标为(-2,0).
如图,在平面直角坐标系xOy中,以原点为位似中心,线段AB与线段A′B′是位似图形,若A(-1,2),B(-1,0),A′(-2,4),则B′的坐标为(-2,0).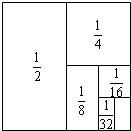 如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的长方形,接着再把面积为$\frac{1}{2}$的一个长方形分成两个面积为$\frac{1}{4}$的长方形,再把面积为$\frac{1}{4}$的一个长方形分成两个面积为$\frac{1}{8}$的长方形,如此进行下去.
如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的长方形,接着再把面积为$\frac{1}{2}$的一个长方形分成两个面积为$\frac{1}{4}$的长方形,再把面积为$\frac{1}{4}$的一个长方形分成两个面积为$\frac{1}{8}$的长方形,如此进行下去.