题目内容
10．已知一次函数y=x+b图象经过两直线l1：x+2y-2=0，l2：2x+y-7=0的交点，则b的值为（ ）| A． | 5 | B． | -5 | C． | 3 | D． | -3 |
分析 先求出两直线l1：x+2y-2=0，l2：2x+y-7=0的交点坐标，再把此点代入y=x+b中，求出b的值即可．
解答 解：根据题意得
$\left\{\begin{array}{l}{x+2y-2=0}\\{2x+y-7=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$，
把（4，-1）代入y=x+b中，得4+b=-1，
解得b=-5．
故选B．
点评 本题考查了两条直线的交点问题，两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解．
练习册系列答案
相关题目
如图，已知∠EFD=∠BCA，BC=EF，AF=DC，则AB=DE．请通过完成以下填空的形式说明理由．
18．
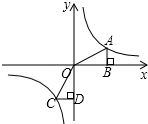如图，A，C是函数$y=\frac{1}{x}$的图象上任意两点，过A作x轴的垂线，垂足为B，过C作y轴的垂线，垂足为D，记Rt△OAB的面积为S1，Rt△COD的面积S2，则（ ）
如图，A，C是函数$y=\frac{1}{x}$的图象上任意两点，过A作x轴的垂线，垂足为B，过C作y轴的垂线，垂足为D，记Rt△OAB的面积为S1，Rt△COD的面积S2，则（ ）| A． | S1＞S2 | B． | S1=S2 | C． | S1＜S2 | D． | S1≥S2 |
5．已知一次函数y=kx+b（k＞0，b＜0），那么一次函数的图象不经过第（ ）象限．
| A． | 一 | B． | 二 | C． | 三 | D． | 四 |
如图，在△ABC中，D为三角形内一点，∠A=35°，∠ABD=20°，∠ACD=25°，BD∥CE，则∠DCE=75°．
19．三角形的两边长分别为4和5，第三边长是方程（x-4）（x-1）=0的解，则这个三角形的周长是（ ）
| A． | 10 | B． | 12 | C． | 13 | D． | 10或13 |