题目内容
9. 某校数学课外实践活动小组想利用所学知识测量南明湖的宽度.如图所示是南明湖的一段,两岸AB∥CD,河对岸E处有一座房子,小组成员用测角仪在F处测得∠EFD=36°,往前走205米后到达点G处,测得∠EGD=72°,请你根据这些数据帮该小组算出湖宽EH(结果精确到0.1).
某校数学课外实践活动小组想利用所学知识测量南明湖的宽度.如图所示是南明湖的一段,两岸AB∥CD,河对岸E处有一座房子,小组成员用测角仪在F处测得∠EFD=36°,往前走205米后到达点G处,测得∠EGD=72°,请你根据这些数据帮该小组算出湖宽EH(结果精确到0.1).(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,cos72°≈0.31,tan72°≈3.08)
分析 根据∠EFD=36°,∠EGD=72°得到∠FEG=36°,即FG=EG=205,根据余弦求出GH,根据勾股定理计算得到答案.
解答 解:∵∠EFD=36°,∠EGD=72°
∴∠FEG=36°,∴FG=EG,
∵FG=205米,∴EG=205米,
∵EH⊥CD,
则cos∠EGH=$\frac{GH}{GE}$,
∴GH=EG•cos∠EGH=205×0.31=63.55,
由勾股定理得,EH=$\sqrt{G{E}^{2}-G{H}^{2}}$≈194.9.
答:河宽约为194.9 m.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念和勾股定理是解题的关键.

练习册系列答案
相关题目
17.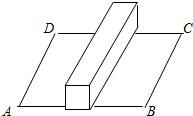 如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
 如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
1.从长度分别为2、3、4、5的4条线段中任取3条,能构成钝角三角形的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
18.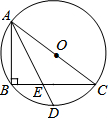 如图,Rt△ABC内接于⊙O,AB=3,BC=4,点D为$\widehat{BC}$的中点,连结AD与BC相交于点E,则DE:AE等于( )
如图,Rt△ABC内接于⊙O,AB=3,BC=4,点D为$\widehat{BC}$的中点,连结AD与BC相交于点E,则DE:AE等于( )
 如图,Rt△ABC内接于⊙O,AB=3,BC=4,点D为$\widehat{BC}$的中点,连结AD与BC相交于点E,则DE:AE等于( )
如图,Rt△ABC内接于⊙O,AB=3,BC=4,点D为$\widehat{BC}$的中点,连结AD与BC相交于点E,则DE:AE等于( )| A. | 3:4 | B. | 1:3 | C. | 2:3 | D. | 2:5 |
 矩形ABCD中,E,F,M分别为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则BF的长为3或4.
矩形ABCD中,E,F,M分别为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则BF的长为3或4.
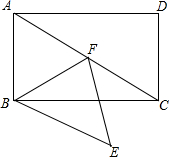 如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.