题目内容
4.为更好地响应丽水市的创国卫活动,某校抽取了九年级部分同学对饮食卫生知识进行了测试,并将测试结果按照A,B,C,D四个等级绘制成如下两个统计图,请结合图中信息解答下列问题: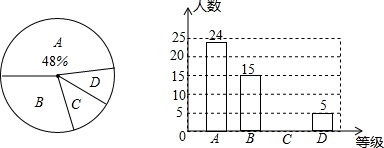
(1)请把条形统计图补充完整,并求出扇形统计图中B部分所对应的圆心角的度数;
(2)该校共有学生1 000人,若把测试结果为A的记为优秀,请根据样本估计全校饮食卫生知识了解情况达到优秀的学生人数是多少?
(3)为进一步提高学生对饮食卫生知识的知晓率,学校又连续组织了两次测试,最后一次达到优秀的学生增加到750人,求平均每次的增长率.
分析 (1)首先根据两个统计图得到总人数,然后求得C组的频数,从而补全条形统计图;
(2)用总人数乘以优秀率即可求得优秀人数;
(3)设平均增长率为为x,根据题意列出方程求解即可;
解答 解:(1)由两个统计图知:A有24人,占48%,
故总人数为24÷48%=50人,
C对应的人数为50-24-15-5=6,
B所对应的圆心角度数为15÷50×360=108°;
(2)1000×$\frac{24}{50}$=480(人);
(3)设平均增长率为x,根据题意得
480(1+x)2=750,
解得x=$\frac{1}{4}$或x=-$\frac{9}{4}$(舍去)
答:平均增长率为25%.
点评 本题考查一元二次方程的应用、条形统计图等知识.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
相关题目
14.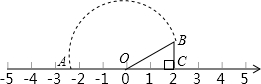 如图所示,点C的表示的数为2,BC=1,以O为圆心,OB为半径画弧,交数轴于点A,则点A表示的数是( )
如图所示,点C的表示的数为2,BC=1,以O为圆心,OB为半径画弧,交数轴于点A,则点A表示的数是( )
 如图所示,点C的表示的数为2,BC=1,以O为圆心,OB为半径画弧,交数轴于点A,则点A表示的数是( )
如图所示,点C的表示的数为2,BC=1,以O为圆心,OB为半径画弧,交数轴于点A,则点A表示的数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | -$\sqrt{3}$ | D. | -$\sqrt{5}$ |
12.下列命题:
①方程x2=x的解是x=1;
②$\sqrt{4}$的算术平方根是$\sqrt{2}$;
③有两边和一角相等的两个三角形全等;
④连接任意四边形各边中点的四边形是平行四边形,
其中真命题有( )
①方程x2=x的解是x=1;
②$\sqrt{4}$的算术平方根是$\sqrt{2}$;
③有两边和一角相等的两个三角形全等;
④连接任意四边形各边中点的四边形是平行四边形,
其中真命题有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
13.满足不等式2x<-1最大整数解的x值是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
14.抛物线y=x2-2x+1向左平移2个单位长度后,所得到的抛物线与x轴的交点坐标为( )
| A. | (-3,0) | B. | (-2,0) | C. | (-1,0) | D. | (3,0) |
 某校数学课外实践活动小组想利用所学知识测量南明湖的宽度.如图所示是南明湖的一段,两岸AB∥CD,河对岸E处有一座房子,小组成员用测角仪在F处测得∠EFD=36°,往前走205米后到达点G处,测得∠EGD=72°,请你根据这些数据帮该小组算出湖宽EH(结果精确到0.1).
某校数学课外实践活动小组想利用所学知识测量南明湖的宽度.如图所示是南明湖的一段,两岸AB∥CD,河对岸E处有一座房子,小组成员用测角仪在F处测得∠EFD=36°,往前走205米后到达点G处,测得∠EGD=72°,请你根据这些数据帮该小组算出湖宽EH(结果精确到0.1).