题目内容
2. 已知,点A(1,3),B(4,0)
已知,点A(1,3),B(4,0)(1)求△AOB的面积;
(2)若点P(m,2),当四边形ABOP的面积是△AOB的面积的2倍时,求m的值.
分析 (1)过点A作作AC⊥OB,垂足为C,由点的坐标的定义可知AC=3,然后依据三角形的面积公式求解即可;
(2)首先根据题意画出图形,如图2所示,由S△APO=SACDO-S△ACP-S△OPD=6列方程求解即可;如图3所示由S△APB=SACDB-S△ACP-S△PBD=6列方程求解即可.
解答 解:(1)过点A作AC⊥OB,垂足为C.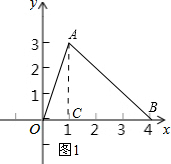
${S}_{△AOB}=\frac{1}{2}OB•AC$=$\frac{1}{2}×4×3$=6.
(2)如图2所示;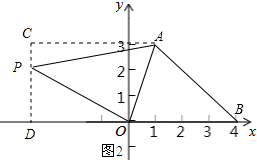
∵四边形ABOP的面积是△AOB的面积的2倍,
∴S△APO=S△AOB=6.
∵S△APO=SACDO-S△ACP-S△OPD,
∴$\frac{1}{2}(-m+1-m)×3$-$\frac{1}{2}×(1-m)×1$-$\frac{1}{2}×$2×(-m)=6.
解得:m=-$\frac{10}{3}$.
如图3所示: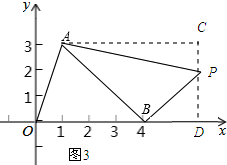
∵四边形ABOP的面积是△AOB的面积的2倍,
∴S△APB=S△ABO=6.
∵S△APB=SACDB-S△ACP-S△PBD,
∴$\frac{1}{2}×(m-4+m-1)×3$-$\frac{1}{2}×1×(m-1)$-$\frac{1}{2}×2×(m-4)$=6.
解得:m=6.
综上所述,m的值为-$\frac{10}{3}$或6.
点评 本题主要考查的是坐标与图形的性质,根据题意画出图形,依据割补法表示三角形APB和△APO的面积是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(-1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为(1,-4).
如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(-1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为(1,-4). 如图,己知直角三角形ABC的顶点A(2,0),B(2,3),A是直角顶点,斜边长为5.画出平面直角坐标系并求顶点C的坐标.
如图,己知直角三角形ABC的顶点A(2,0),B(2,3),A是直角顶点,斜边长为5.画出平面直角坐标系并求顶点C的坐标.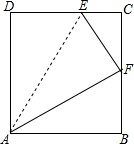 如图,在矩形ABCD中,E是DC上的一点,以线段AE为折痕对折,使点D落在BC边上的中点F处,且EF平分∠AEC,求证:AF是∠EAB的平分线.
如图,在矩形ABCD中,E是DC上的一点,以线段AE为折痕对折,使点D落在BC边上的中点F处,且EF平分∠AEC,求证:AF是∠EAB的平分线.