题目内容
9. 如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(-1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为(1,-4).
如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(-1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为(1,-4).
分析 作AC⊥x轴于C,利用点A、B的坐标得到AC=2,BC=4,根据旋转的定义,可把Rt△BAC绕点B顺时针旋转90°得到△BA′C′,如图,利用旋转的性质得BC′=BC=4,A′C′=AC=2,于是可得到点A′的坐标.
解答 解:作AC⊥x轴于C,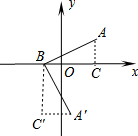
∵点A、B的坐标分别为(3,2)、(-1,0),
∴AC=2,BC=3+1=4,
把Rt△BAC绕点B顺时针旋转90°得到△BA′C′,如图,
∴BC′=BC=4,A′C′=AC=2,
∴点A′的坐标为(1,-4).
故答案为(1,-4).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.解决本题的关键是把线段的旋转问题转化为直角三角形的旋转.

练习册系列答案
相关题目
19.代数式$\frac{a-b}{7}$,0,3a,abc,$\frac{b}{a}$中,单项式有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
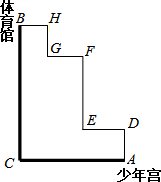 如图,粗线A→C→B和细线A→D→E→F→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
如图,粗线A→C→B和细线A→D→E→F→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.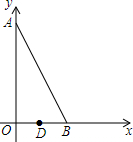 如图,在平面直角坐标系xOy中,点A在y轴上,点B在x轴上,∠ABO=60°,若点D(1,0)且BD=2OD.把△ABO绕着点D逆时针旋转m°(0<m<180)后,点B恰好落在初始Rt△ABO的边上,此时的点B记为B′,则点B′的坐标为(2,$\sqrt{3}$)或(0,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,点A在y轴上,点B在x轴上,∠ABO=60°,若点D(1,0)且BD=2OD.把△ABO绕着点D逆时针旋转m°(0<m<180)后,点B恰好落在初始Rt△ABO的边上,此时的点B记为B′,则点B′的坐标为(2,$\sqrt{3}$)或(0,$\sqrt{3}$). 已知,点A(1,3),B(4,0)
已知,点A(1,3),B(4,0) (1)写出图中A,B,C各点的坐标;
(1)写出图中A,B,C各点的坐标;