Question

14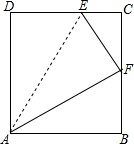．如图，在矩形ABCD中，E是DC上的一点，以线段AE为折痕对折，使点D落在BC边上的中点F处，且EF平分∠AEC，求证：AF是∠EAB的平分线．

Answer 1

分析 根据矩形的性质得到CD∥AB，由平行线的性质得到∠BAE+∠AEC=180°，根据折叠的性质得到∠AFE=∠D=90°，求得∠FAE+∠AEF=90°，∠FAB+∠CEF=90°，根据角平分线的定义得到∠AEF=∠CEF，即可得到结论．

解答 证明：在矩形ABCD中，
∵CD∥AB，
∴∠BAE+∠AEC=180°，
∵△AEF是△ADE沿着AE折叠得到的，
∴∠AFE=∠D=90°，
∴∠FAE+∠AEF=90°，
∴∠FAB+∠CEF=90°，
∵EF平分∠AEC，
∴∠AEF=∠CEF，
∴∠EAF=∠BAF，
∴AF是∠EAB的平分线．

点评 本题考查了翻折变换-折叠问题，矩形的性质，角平分线的定义，熟练掌握折叠的性质是解题的关键．