题目内容
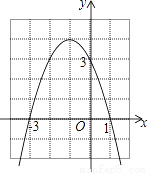
如图是二次函数y=ax2+bx+c的图象，下列结论： ①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为﹣1；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】试题解析：∵抛物线的顶点坐标为（-1，4），∴二次三项式ax2+bx+c的最大值为4，①正确；
∵x=2时，y＜0，∴4a+2b+c＜0，②正确；
根据抛物线的对称性可知，一元二次方程ax2+bx+c=1的两根之和为-2，③错误；
使y≤3成立的x的取值范围是x≥0或x≤-2，④错误，
故选B．
练习册系列答案
阅读快车系列答案
相关题目
抛物线y=x2－2x+3的顶点坐标是_______．
(1，2)
【解析】试题解析：∵y=x2-2x+3=x2-2x+1-1+3=（x-1）2+2，
∴抛物线y=x2-2x+3的顶点坐标是（1，2） 已知不论x为何值，x2-kx-15=(x+5)(x-3)，则k值为（ ）
A. 2 B. -2 C. 5 D. -3
B
【解析】∵x2-kx-15=(x+5)(x-3)=x2+2x-15，
∴k=-2.
故选B. 已知二次函数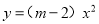
的图象开口向下，则m的取值范围是________
m＜2
【解析】由二次函数的图象的开口方向，知m-2＜0，确定m的取值范围m＜2．
故答案为：m＜2． 抛物线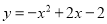
经过平移得到
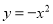，平移方法是（ ）
A. 向右平移1个单位，再向上平移1个单位
B. 向右平移1个单位，再向下平移1个单位
C. 向左平移1个单位，再向上平移1个单位
D. 向左平移1个单位，再向下平移1个单位
C
【解析】由抛物线得到顶点坐标为（1，-1），而平移后抛物线的顶点坐标为（0，0），根据顶点坐标的变化寻找平移方法为：向左平移1个单位，再向上平移1个单位．
故选：C． 如图，抛物线
与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F.已知点A的坐标为（﹣1，0）.
（1）求该抛物线的解析式及顶点M的坐标；
（2）求△EMF与△BNF的面积之比.
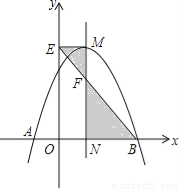
（1），（1，4）；（2）.
【解析】试题分析：（1）直接将（﹣1，0）代入求出即可，再利用配方法求出顶点坐标.
（2）利用EM∥BN，则△EMF∽△BNF，进而求出△EMF与△BNE的面积之比．
试题解析：【解析】
（1）∵点A在抛物线上，
∴，解得：c=3，
∴抛物线的解析式为.
∵，
∴抛物线的顶点M（1，4）；
（2）∵A（﹣1，0），抛物... 如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3，那么c的值等于（ ）
A. 8
B. 14
C. 8或14
D. -8或-14
C
【解析】根据题意，得
，
解得c=8或14．
故选：C． 将二次函数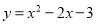
化成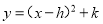
形式，则h+k结果为（ ）
A. -5
B. 5
C. -3
D. 3
C
【解析】．
则h=1，k=-4，
∴h+k=-3．
故选：C． 如图所示，已知二次函数y＝ax2+bx+c(a≠0)的图象的顶点p的横坐标是4，图象与x轴交于点A(m，0)和点B，且点A在点B的左侧，那么线段AB的长是____．(用含字母m的代数式表示)
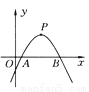
8－2m
【解析】因为二次函数y=ax²+bx+c(a≠0)的图象的顶点P的横坐标是4，
所以抛物线对称轴所在直线为x=4，交x轴于点D，
所以A.B两点关于对称轴对称，
因为点A(m,0)，且m<4，即AD=4-m，
所以AB=2AD=2(4-m)=8-2m，
故答案为：8-2m.