题目内容
观察下面算962×95+962×5的解题过程，其中最简单的方法是( )
A. 962×95+962×5＝962×(95+5)＝962×100＝96200
B. 962×95+962×5＝962×5×(19+1)＝962×(5×20) ＝96200
C. 962×95+962×5＝5×(962×19+962)＝5×(18278+962)＝96200
D. 962×95+962×5＝91390+4810＝96200
A
【解析】计算962×95+962×5的值，最简单的方法先提取公因式962，即962×95+962×5＝962×(95+5)＝962×100＝96200，故选A.
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
河堤横断面如图所示，堤高BC=6米，迎水坡AB的坡比为1：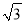 
则AB的长为_______
12米
【解析】试题分析：根据BC=6m，坡比为1： 可得：AC=6m，最后根据Rt△ABC的勾股定理可得：AB=12米． 如果x+y=5,xy=2,求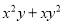
和
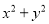的值
10；21.
【解析】试题分析：（1）因式分解后直接代入求值即可；（2）化为（x+y）2-2xy后代入求值即可.
试题解析：
∵x+y=5，xy=2，
∴=xy（x+y）=2×5=10；
=（x+y）2-2xy=52-2×2=25-4=21. 若关于x的多项式3x2+mx+n分解因式的结果为(3x+2)(x-1)，求m、n的值.
m=-1,n=-2.
【解析】试题分析：把(3x+2)(x-1)利用多项式乘以多项式的法则展开，与多项式3x2+mx+n比较，即可得m、n的值.
试题解析：
由题意可得：(3x+2)(x-1)=3x2+2x-3x-2=3x2-x-2=3x2+mx+n，
所以m=-1,n=-2. 已知不论x为何值，x2-kx-15=(x+5)(x-3)，则k值为（ ）
A. 2 B. -2 C. 5 D. -3
B
【解析】∵x2-kx-15=(x+5)(x-3)=x2+2x-15，
∴k=-2.
故选B. 已知m，n是关于x的方程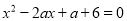
的两实根，求
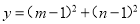的最小值．
8
【解析】试题分析：根据方程有两个根，利用根的判别式求出a的取值范围，再根据根与系数的关系求出m+n与mn的值，然后把整理成m+n与mn的形式，代入进行计算求解．
试题解析：依题意△=≥0，
即，
∴a≤-2或a≥3，
由m+n=2a，mn=a+6，
即
=
=
=，
∴a=3时，y的最小值为8．
故答案为：8． 已知二次函数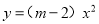
的图象开口向下，则m的取值范围是________
m＜2
【解析】由二次函数的图象的开口方向，知m-2＜0，确定m的取值范围m＜2．
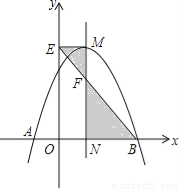
故答案为：m＜2． 如图，抛物线
与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F.已知点A的坐标为（﹣1，0）.
（1）求该抛物线的解析式及顶点M的坐标；
（2）求△EMF与△BNF的面积之比.
（1），（1，4）；（2）.
【解析】试题分析：（1）直接将（﹣1，0）代入求出即可，再利用配方法求出顶点坐标.
（2）利用EM∥BN，则△EMF∽△BNF，进而求出△EMF与△BNE的面积之比．
试题解析：【解析】
（1）∵点A在抛物线上，
∴，解得：c=3，
∴抛物线的解析式为.
∵，
∴抛物线的顶点M（1，4）；
（2）∵A（﹣1，0），抛物... 一项工作，若甲单独完成需x小时，则甲每小时完成工作的________.若甲、乙合作 需8小时完成，则乙每小时完成工作的_______.
【解析】一项工作，若甲单独完成需x小时，则甲每小时完成工作的，
若甲、乙合作需8小时完成，则乙每小时完成工作的，
故答案为： ， .