题目内容
12.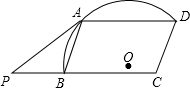 如图,在?ABCD中,∠ABC=70°,半径为r的⊙O经过点A,B,D,$\widehat{AD}$的长是$\frac{πr}{2}$,延长CB至点P,使得PB=AB.判断直线PA与⊙O的位置关系,并说明理由.
如图,在?ABCD中,∠ABC=70°,半径为r的⊙O经过点A,B,D,$\widehat{AD}$的长是$\frac{πr}{2}$,延长CB至点P,使得PB=AB.判断直线PA与⊙O的位置关系,并说明理由.
分析 连接OA、OD,由等腰三角形的性质得出∠P=∠BAP,由三角形的外角性质得出∠BAP=$\frac{1}{2}$∠ABC=35°,由弧长公式求出∠AOD=90°,由等腰三角形的性质得出∠OAD=∠ODA=45°,由平行四边形的性质求出∠BAD=110°,得出∠BAO=65°,因此∠OAP=35°+65°=100°>90°,即可得出结论.
解答 解:直线PA与⊙O相交;理由如下: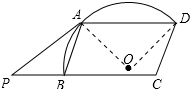
连接OA、OD,如图所示:
∵PB=AB,
∴∠P=∠BAP,
∵∠ABC=∠P+∠BAP,
∴∠BAP=$\frac{1}{2}$∠ABC=35°,
设∠AOD的度数为n,
∵$\widehat{AD}$的长=$\frac{nπr}{180}$=$\frac{πr}{2}$,
解得:n=90,
∴∠AOD=90°,
∵OA=OD,
∴∠OAD=∠ODA=45°,
∵四边形ABCD是平行四边形,
∴∠BAD=180°-∠ABC=110°,
∴∠BAO=∠BAD-∠OAD=110°-45°=65°,
∴∠OAP=35°+65°=100°>90°,
∴直线PA与⊙O相交.
点评 本题考查了直线与圆的位置关系、等腰三角形的性质、三角形的外角性质、弧长公式、平行四边形的性质;熟练掌握平行四边形的性质,由弧长公式求出∠AOD的度数是解决问题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
2.下面哪个点在函数y=-2x+3的图象上( )
| A. | (3,1) | B. | (3,0) | C. | (1,1) | D. | (1,3) |
7.某公司欲招聘一名工作人员,对甲应聘者进行面试和笔试,面试成绩为85分,笔试成绩为90分.若公司分别赋予面试成绩和笔试成绩7和3的权,则下列算式表示甲的平均成绩的是( )
| A. | $\frac{85+90}{2}$ | B. | $\frac{85×7+90×3}{2}$ | C. | $\frac{85×7+90×3}{10}$ | D. | $\frac{85×0.7+90×0.3}{10}$ |
2.方程2(10-0.5x)+(3x+2)=10的解为( )
| A. | 8 | B. | -8 | C. | 6 | D. | -6 |
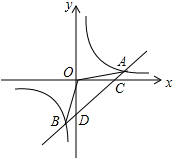 如图,一次函数y=x+b和反比例函数$y=\frac{k}{x}(k≠0)$交于点A(2,1).
如图,一次函数y=x+b和反比例函数$y=\frac{k}{x}(k≠0)$交于点A(2,1).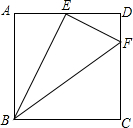 如图,在正方形ABCD中,边长为4,点E、F分别在边AD和CD上,其中AE=2,DF=1,判断BE与EF的位置关系并说明理由.
如图,在正方形ABCD中,边长为4,点E、F分别在边AD和CD上,其中AE=2,DF=1,判断BE与EF的位置关系并说明理由.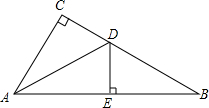 如图,在Rt△ABC中,∠C=90°,DE垂直平分AB分别交BC、AB于点D、E,且CD=DE,求∠B的度数.
如图,在Rt△ABC中,∠C=90°,DE垂直平分AB分别交BC、AB于点D、E,且CD=DE,求∠B的度数.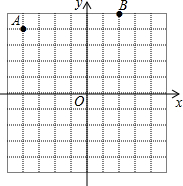 如图,平面直角坐标系中,点A的坐标是(-4,4),点B的坐标是(2,5).
如图,平面直角坐标系中,点A的坐标是(-4,4),点B的坐标是(2,5).