题目内容
10.化简:$\frac{{x}^{2}}{x-3}+\frac{6x-9}{3-x}$=x-3.分析 先化为同分母的分式,再进行加减即可.
解答 解:原式=$\frac{{x}^{2}}{x-3}$-$\frac{6x-9}{x-3}$
=$\frac{{x}^{2}-6x+9}{x-3}$
=$\frac{(x-3)^{2}}{x-3}$
=x-3.
故答案为x-3.
点评 本题考查了分式的加减,分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
15.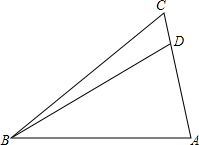 如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
(1)请用直尺和圆规在图中直接作出∠A的平分线AE交BD于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,求出∠AED的度数.
 如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.(1)请用直尺和圆规在图中直接作出∠A的平分线AE交BD于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,求出∠AED的度数.
2.方程2(10-0.5x)+(3x+2)=10的解为( )
| A. | 8 | B. | -8 | C. | 6 | D. | -6 |
19.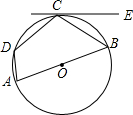 如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
 如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )| A. | 145° | B. | 125° | C. | 90° | D. | 80° |
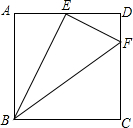 如图,在正方形ABCD中,边长为4,点E、F分别在边AD和CD上,其中AE=2,DF=1,判断BE与EF的位置关系并说明理由.
如图,在正方形ABCD中,边长为4,点E、F分别在边AD和CD上,其中AE=2,DF=1,判断BE与EF的位置关系并说明理由.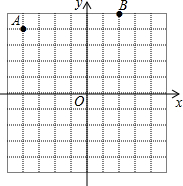 如图,平面直角坐标系中,点A的坐标是(-4,4),点B的坐标是(2,5).
如图,平面直角坐标系中,点A的坐标是(-4,4),点B的坐标是(2,5).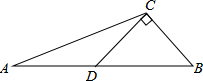 如图,CD是△ABC的中线,CD⊥CB,∠ACD=30°,求证:AC=2BC.
如图,CD是△ABC的中线,CD⊥CB,∠ACD=30°,求证:AC=2BC.