题目内容
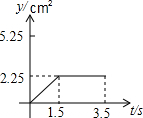
10.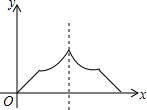 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )| A. | 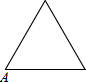 | B. | 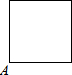 | C. |  | D. | 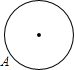 |
分析 根据等边三角形,正方形,矩形,圆的性质,分析得到y随x的增大的变化关系,然后选择答案即可.
解答 解:A、等边三角形,点P在开始与结束的两边上直线变化,
在点A的对边上时,设等边三角形的边长为a,
则y=$\sqrt{{(\frac{\sqrt{3}}{2}a)}^{2}{+(\frac{3}{2}a-x)}^{2}}$(a<x<2a),不符合题干图象;
B、正方形,点P在开始与结束的两边上直线变化,
在另两边上,先变速增加至∠A的对角顶点,再变速减小至另一顶点,符合题干图象;
C、矩形,点P在开始与结束的两边上直线变化,
在另两边上,先变速增加至∠A的对角顶点,再变速减小至另一顶点,但是俩长度不同,题干图象不符合
D、圆,MP的长度,先变速增加至MP为直径,然后再变速减小至点P回到点M,题干图象不符合;
故选B.
点评 本题考查了动点问题函数图象,熟练掌握等边三角形,矩形,正方形以及圆的性质,理清点P在各边时MP的长度的变化情况是解题的关键.

练习册系列答案
相关题目
13.若k<$\sqrt{90}$<k+1(k是整数),则k=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
19.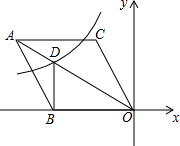 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )| A. | 6$\sqrt{3}$ | B. | -6$\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | -12$\sqrt{3}$ |
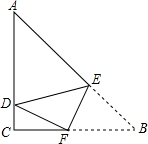 如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E、F分别为AB、AC上的点,沿直线EF将∠B折叠,使点B恰好落在AC上的D处,当△ADE恰好为直角三角形时,BE的长为$\frac{15}{4}$或$\frac{30}{7}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E、F分别为AB、AC上的点,沿直线EF将∠B折叠,使点B恰好落在AC上的D处,当△ADE恰好为直角三角形时,BE的长为$\frac{15}{4}$或$\frac{30}{7}$.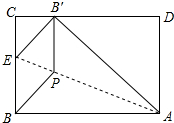 将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP.已知BC=3,CB′=1,下列结论:
将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP.已知BC=3,CB′=1,下列结论: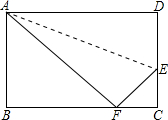 如图,在矩形ABCD中,AB=6cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是24cm2.则AD=10cm,CE=$\frac{8}{3}$cm.
如图,在矩形ABCD中,AB=6cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是24cm2.则AD=10cm,CE=$\frac{8}{3}$cm.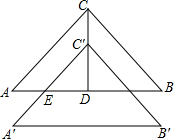 如图,Rt△ABC中,∠ACB=90°,CA=CB,AB=8,D是线段AB上的一个动点,将Rt△ABC由点C到点D的方向平移2个单位得到Rt△A′B′C′,且C′A′与AB交于点E.
如图,Rt△ABC中,∠ACB=90°,CA=CB,AB=8,D是线段AB上的一个动点,将Rt△ABC由点C到点D的方向平移2个单位得到Rt△A′B′C′,且C′A′与AB交于点E.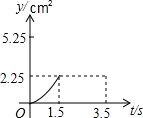
 如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.