题目内容
1.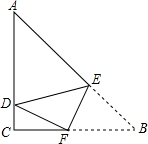 如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E、F分别为AB、AC上的点,沿直线EF将∠B折叠,使点B恰好落在AC上的D处,当△ADE恰好为直角三角形时,BE的长为$\frac{15}{4}$或$\frac{30}{7}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E、F分别为AB、AC上的点,沿直线EF将∠B折叠,使点B恰好落在AC上的D处,当△ADE恰好为直角三角形时,BE的长为$\frac{15}{4}$或$\frac{30}{7}$.
分析 先在Rt△ABC中利用勾股定理求出AC=6cm,再根据折叠的性质得到BE=DE,直线EF将∠B折叠,使点B恰好落在BC上的D处,△ADE恰好为直角三角形,有两种可能:①∠ADE=90°,②∠AED=90°,设BE=x,运用三角形相似列比例式解方程即可得解.
解答 解:在Rt△ABC中,∵∠C=90°,AC=8cm,AB=10cm,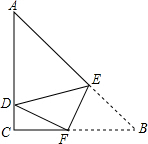
∴BC=6cm.
直线EF将∠B折叠,使点B恰好落在BC上的D处,当△ADE恰好为直角三角形时,
根据折叠的性质:BE=DE
设BE=x,则DE=x,AE=10-x
①当∠ADE=90°时,则DE∥BC,
∴$\frac{DE}{CB}=\frac{AE}{AB}$
∴$\frac{x}{6}=\frac{10-x}{10}$
解得:x=$\frac{15}{4}$
②当∠AED=90°时,
则△AED∽△ACB
∴$\frac{DE}{BC}=\frac{AE}{AC}$
∴$\frac{x}{6}=\frac{10-x}{8}$
解得:x=$\frac{30}{7}$
故所求BE的长度为:$\frac{15}{4}$或$\frac{30}{7}$.
故答案为:$\frac{15}{4}$或$\frac{30}{7}$.
点评 本题考查了折叠的性质,勾股定理以及相似三角形的判定与性质,能够全面的思考问题进行分类讨论是本题的关键.

练习册系列答案
相关题目
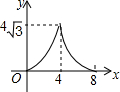
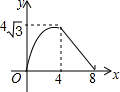
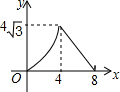
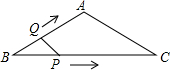 如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以$\sqrt{3}$cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以$\sqrt{3}$cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )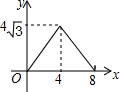
 如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.
如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.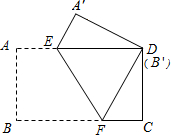 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF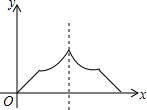 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )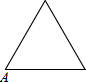
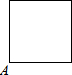

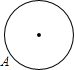
 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是3.
如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是3.