题目内容
5.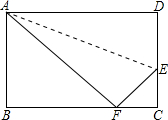 如图,在矩形ABCD中,AB=6cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是24cm2.则AD=10cm,CE=$\frac{8}{3}$cm.
如图,在矩形ABCD中,AB=6cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是24cm2.则AD=10cm,CE=$\frac{8}{3}$cm.
分析 由在长方形ABCD中,AB=6cm,△ABF的面积是24cm2,即可求得BF的长,易得AD=AF,DE=EF,即可求得AF的长,然后得出AD的长,设EC=xcm,则EF=DE=(6-x)cm.由勾股定理得:CE2+CF2=EF2求出x的值即可.
解答 解:(1)∵ABCD是长方形,
∴△ABF是直角三角形,
∵△ABF面积是24cm2,
∴$\frac{1}{2}$AB•BF=24.
∵AB=6cm,
∴BF=8cm,
由题意知,△ADE和△AFE重合,
则△ADE≌△AFE,
则AD=AF,DE=EF.
在Rt△ABF中,由勾股定理得
AF=$\sqrt{A{B}^{2+}B{F}^{2}}$=10(cm).
则AD=10cm,
∵BC=AD=10cm,
∴CF=BC-BF=2cm
设EC=xcm,则EF=DE=(6-x)cm.
由勾股定理得:CE2+CF2=EF2
∴x2+22=(6-x)2
解得:x=$\frac{8}{3}$
∴CE=$\frac{8}{3}$cm.
故答案为:10;$\frac{8}{3}$.
点评 此题考查了矩形的性质、折叠的性质以及勾股定理等知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
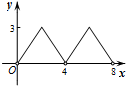
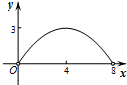
10.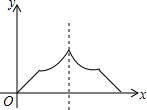 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )| A. |  | B. |  | C. |  | D. |  |
14.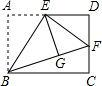 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )
 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{6}$ | D. | 2$\sqrt{3}$ |
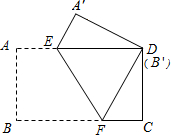 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF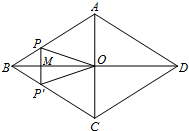 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )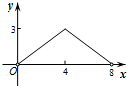
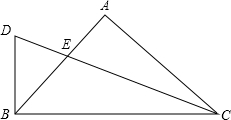 如图,在△ABC中,AB=AC,∠A=90°,CE平分∠ACB,交AB于点E,延长CE作DB⊥BC,垂足为B,则$\frac{CE}{ED}$=$\sqrt{2}$+1.
如图,在△ABC中,AB=AC,∠A=90°,CE平分∠ACB,交AB于点E,延长CE作DB⊥BC,垂足为B,则$\frac{CE}{ED}$=$\sqrt{2}$+1.