题目内容
4.先化简,再求值:$\frac{b}{{a}^{2}-{b}^{2}}$÷($1-\frac{a}{a+b}$),其中a=2016,b=2015.分析 先根据分式混合运算的法则把原式进行化简,再把a、b的值代入进行计算即可.
解答 解:原式=$\frac{b}{(a+b)(a-b)}$÷$\frac{b}{a+b}$
=$\frac{b}{(a+b)(a-b)}$•$\frac{a+b}{b}$
=$\frac{1}{a-b}$,
当a=2016,b=2015时,原式=$\frac{1}{2016-2015}$=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
12.下列根式中属最简二次根式的是( )
| A. | $\sqrt{13}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\frac{1}{{\sqrt{2}}}$ |
14.若实数m=$\sqrt{18}-\sqrt{8}$,则估计m的值所在范围正确的是( )
| A. | 1<m<2 | B. | 2<m<3 | C. | 3<m<4 | D. | 4<m<5 |
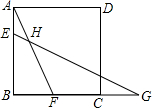 如图,在边长为6的正方形ABCD中,E、F、G分别是AB、BC、和BC延长线上的点,若AE=BF=CG=2,连接EG、AF交于点H,则AH的长为$\frac{4\sqrt{10}}{5}$.
如图,在边长为6的正方形ABCD中,E、F、G分别是AB、BC、和BC延长线上的点,若AE=BF=CG=2,连接EG、AF交于点H,则AH的长为$\frac{4\sqrt{10}}{5}$.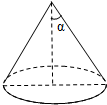 如图,圆锥的母线长为11cm,侧面积为55πcm2,设圆锥的母线与高的夹角为α,则cosα的值为$\frac{4\sqrt{6}}{11}$.
如图,圆锥的母线长为11cm,侧面积为55πcm2,设圆锥的母线与高的夹角为α,则cosα的值为$\frac{4\sqrt{6}}{11}$. 如图,矩形ABCD的对角线AC,BD的和是20,且BC=2AB,则AB的长度为2$\sqrt{5}$.
如图,矩形ABCD的对角线AC,BD的和是20,且BC=2AB,则AB的长度为2$\sqrt{5}$.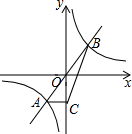 如图,正比例函数y=kx(k>0)和反比例函数y=$\frac{6}{x}$的图象交于A、B两点,过点A作AC⊥y轴于点C,则△ABC的面积为6.
如图,正比例函数y=kx(k>0)和反比例函数y=$\frac{6}{x}$的图象交于A、B两点,过点A作AC⊥y轴于点C,则△ABC的面积为6.