题目内容
15.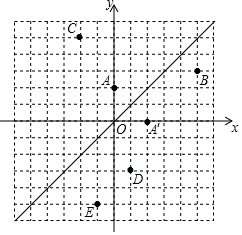 如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.实验与探究:
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出它们的坐标:B′(3,5)、C′(5,-2);
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为(b,a)(不必证明);
运用与拓广:
(3)已知两点D(1,-3)、E(-1,-5),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小.
分析 (1)根据点关于直线对称的定义,作出B、C两点关于直线l的对称点B′、C′,写出坐标即可.
(2)通过观察即可对称结论.
(3)作点E关于直线l的对称点E′((-5,-1),连接DE′交直线l于Q,此时QE+QD的值最小.
解答 解:(1)B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置如图所示.
B′(3,5),C′(5,-2).
故答案为B′(3,5),C′(5,-2).
(2)由(1)可知点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为P′(b,a).
(3)作点E关于直线l的对称点E′((-5,-1),连接DE′交直线l于Q,此时QE+QD的值最小.
点评 本题考查轴对称-最短问题、坐标与图形变化-对称、两点之间线段最短等知识,解题的关键是理解轴对称的定义,学会利用对称解决最短问题,属于中考常考题型.

练习册系列答案
相关题目
4.已知在△ABC中∠A=40°,∠B=50°,则△ABC为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 以上都有可能 |
5.某人去水果批发市场采购苹果,他看中了A、B两家苹果,这两家苹果品质一样,零售价为6元/千克,批发价各不相同.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
(1)如果他批发600千克苹果,则他在A、B两家批发分别需要多少元?
(2)如果他批发x千克苹果(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
| 数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
| 价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(2)如果他批发x千克苹果(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
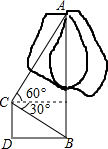 为改变哈尔滨市的交通状况,在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°,那么距离B点7米远,才是安全区域.(结果保留整数,$\sqrt{3}$≈1.732)
为改变哈尔滨市的交通状况,在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°,那么距离B点7米远,才是安全区域.(结果保留整数,$\sqrt{3}$≈1.732)