题目内容
4．方程x2-4x+3=0的根的情况是（ ）| A． | 有两个相等的实数根 | B． | 只有一个实数根 | ||
| C． | 没有实数根 | D． | 有两个不相等的实数根 |
分析 先计算判别式的值，然后根据判别式的意义进行判断．
解答 解：△=（-4）2-4×1×3=4＞0，
所以方程有两个不相等的两个实数根．
故选D．
点评 本题考查了根的判别式：用一元二次方程根的判别式（△=b2-4ac）判断方程的根的情况．一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的两个实数根；当△=0时，方程有两个相等的两个实数根；当△＜0时，方程无实数根．
练习册系列答案
星级口算天天练系列答案
相关题目
分别计算：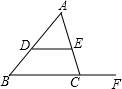
如图，DE∥BC，CF为BC的延长线，若∠ADE=50°，∠ACF=110°，则∠A=60°．
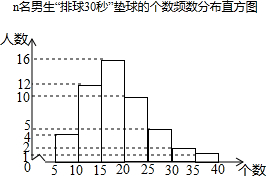某校为了预测九年级男生“排球30秒”对墙垫球的情况，从本校九年级随机抽取了n名男生进行该项目测试，并绘制出如下的频数分布直方图，其中从左到右依次分为七个组（每组含最小值，不含最大值）．根据统计图提供的信息解答下列问题：
9．
如图，直线AB∥CD，AC⊥BC于点C，若∠1=40°，则∠2的度数是（ ）
如图，直线AB∥CD，AC⊥BC于点C，若∠1=40°，则∠2的度数是（ ）| A． | 50° | B． | 40° | C． | 80° | D． | 60° |
如图，已知∠1=70°，∠2=50°，∠D=70°，AE∥BC，求∠C的度数．
解不等式或不等式组．