题目内容
11.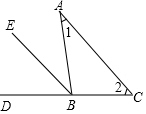 如图,已知在△ABC中,∠1=∠2.
如图,已知在△ABC中,∠1=∠2.(1)请你添加一个与直线AC有关的条件,由此可得出BE是△ABC的外角平分线;
(2)请你添加一个与∠1有关的条件,由此可得出BE是△ABC的外角平分线;
(3)如果“已知在△ABC中,∠1=∠2不变”,请你把(1)中添加的条件与所得结论互换,所得的命题是否是真命题,理由是什么?
分析 (1)-(2)要使BE是△ABC的外角平分线,结合三角形的外角的性质∠ABD=∠1+∠2,∠ABE=∠DBE,∠1=∠2,即可证明∠ABE=∠1=∠DBE=∠2,进一步可得BE∥AC;
(3)根据平行线的性质和三角形的外角的性质即可证明.
解答 解:(1)AC∥BE;
(2)∠1=∠ABE或∠1=∠DBE;
(3)是真命题,理由如下:
∵BE是△ABC的外角平分线,
∴∠ABE=∠DBE,
又∵∠ABD是三角形ABC的外角,
∴∠ABD=∠1+∠2,
即∠ABE+∠DBE=∠1+∠2,
又∵∠ABE=∠DBE,∠1=∠2,
∴∠ABE=∠1,
∴AC∥BE.
点评 本题考查了角平分线定义、平行线的性质和三角形的外角的性质,熟练掌握三角形的外角的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
 如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
13.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上的中线的比为( )
| A. | 2:3 | B. | 4:16 | C. | 3:2 | D. | 16:4 |
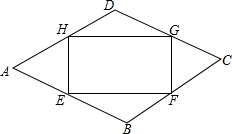 如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH,其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°
如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH,其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°