题目内容
5.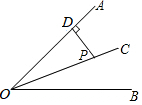 如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,垂足为D,若PD=$\sqrt{3}$,则点P到OB的距离是$\sqrt{3}$.
如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,垂足为D,若PD=$\sqrt{3}$,则点P到OB的距离是$\sqrt{3}$.
分析 可过点P作PE⊥OB,由角平分线的性质可得,PD=PE,进而可得出结论.
解答 解:如图,过点P作PE⊥OB,
∵OC是∠AOB的平分线,点P在OC上,且PD⊥OA,PE⊥OB,
∴PE=PD,
又∵PD=$\sqrt{3}$,
∴PE=PD=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了角平分线的性质;要熟练掌握角平分线的性质,即角平分线上的点到角两边的距离相等.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
16. 如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
 如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
10.将分式$\frac{x+y}{{x}^{2}{+y}^{2}}$中x、y的值均变为原来的2倍,则分式的值( )
| A. | 缩小2倍 | B. | 扩大2倍 | C. | 不变 | D. | 不能确定 |
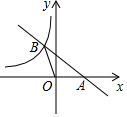 如图,直线y=-$\frac{1}{2}$x+b与x轴交于点A,与双曲线y=-$\frac{4}{x}$(x<0)交于点B,若S△AOB=2,则b的值是( )
如图,直线y=-$\frac{1}{2}$x+b与x轴交于点A,与双曲线y=-$\frac{4}{x}$(x<0)交于点B,若S△AOB=2,则b的值是( )