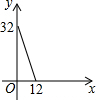题目内容
7.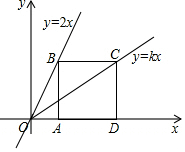 如图,边长为2的正方形ABCD的边AD在x轴的正半轴上,点B和点C分别在直线y=2x和直线y=kx上,则k的值是( )
如图,边长为2的正方形ABCD的边AD在x轴的正半轴上,点B和点C分别在直线y=2x和直线y=kx上,则k的值是( )| A. | 2 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
分析 根据正方形的边长结合一次函数图象上点的坐标特征可找出点B、C的坐标,结合BC=2即可得出关于k的分式方程,解之即可得出结论.
解答 解:∵正方形ABCD的边长为2,
∴AB=CD=2,
∴点B的坐标为(1,2),点B的坐标为($\frac{2}{k}$,2).
∵BC=2,
∴$\frac{2}{k}$-1=2,
解得:k=$\frac{2}{3}$,
经检验,k=$\frac{2}{3}$是原分式方程的解.
故选C.
点评 本题考查了一次函数图象上点的坐标特征以及正方形的性质,根据正方形的边长结合一次函数图象上点的坐标特征表示出点B、C的坐标是解题的关键.

练习册系列答案
相关题目
17.已知关于x的方程2(x+m)-4=0的解是x=2,则m的值为( )
| A. | 1 | B. | 0 | C. | -1 | D. | -$\frac{1}{3}$ |
16. 如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
 如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
 如图,在正方形网格中画的是某校的平面示意图,若花坛与教学楼的坐标分别为(3,-2),(6,1),则实验楼的坐标是(0,0).
如图,在正方形网格中画的是某校的平面示意图,若花坛与教学楼的坐标分别为(3,-2),(6,1),则实验楼的坐标是(0,0).
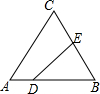 如图,在△ABC中,AC=BC=10,AB=12,D是AB上的一点(不与A、B重合),DE⊥BC,垂足为点E,设BD=x,四边形ACED的周长为y,则下列图象大致反映y与x之间的函数关系的是( )
如图,在△ABC中,AC=BC=10,AB=12,D是AB上的一点(不与A、B重合),DE⊥BC,垂足为点E,设BD=x,四边形ACED的周长为y,则下列图象大致反映y与x之间的函数关系的是( )