题目内容
13.点P(m,n)既在反比例函数y=$\frac{2}{x}$(x>0)的图象上,又在一次函数y=-x-2的图象上,则以m,n为根的一元二次方程为x2+2x+2=0.分析 由于P点是反比例函数与一次函数的交点,因此P点坐标同时满足两个函数的解析式.将P点代入反比例函数解析式中,可得出m、n的乘积;将P点坐标代入一次函数的解析式中,可得出m、n的和;根据韦达定理即可求出以m、n为根的一元二次方程.
解答 解:将P(m,n)代入y=$\frac{2}{x}$中,得:mn=2;
将P(m,n)代入y=-x-2中,得:m+n=2;
根据一元二次方程根与系数的关系可知:以m、n为根的一元二次方程为:x2+2x+2=0.
故答案为:x2+2x+2=0
点评 本题主要考查了反比例函数与一次函数的交点问题,关键是根据一元二次方程根与系数的关系解答.

练习册系列答案
相关题目
6.根据有关资料显示,2015年广东省财政收入约为20934亿元,突破2万亿大关,财政支出民生实事类占近七成,数据20934亿用科学记数法表示为( )
| A. | 2.0934×1012 | B. | 2.0934×1013 | C. | 20.934×1011 | D. | 20934×108 |
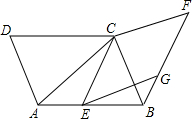 如图,点E是平行四边形ABCD的边AB上的任意一点(不包含端点A,B),分别连接AC,CE,以CE为边作菱形ECFG,再连接BG,已知AB=AC,∠CEG=∠CAB,则下列结论①EG⊥BC,②∠EGB=∠F,③∠CBG=∠CAB,④∠GEB=∠ACE中,一定成立的有②③④(填序号).
如图,点E是平行四边形ABCD的边AB上的任意一点(不包含端点A,B),分别连接AC,CE,以CE为边作菱形ECFG,再连接BG,已知AB=AC,∠CEG=∠CAB,则下列结论①EG⊥BC,②∠EGB=∠F,③∠CBG=∠CAB,④∠GEB=∠ACE中,一定成立的有②③④(填序号). 如图,△ABC为等边三角形,∠ABC的平分线与∠ACB的平分线交于点O,过点O作平行于BC的直线,交AB于M,交AC于N,连接AO,则图中等腰三角形(不含等边三角形)的个数有( )
如图,△ABC为等边三角形,∠ABC的平分线与∠ACB的平分线交于点O,过点O作平行于BC的直线,交AB于M,交AC于N,连接AO,则图中等腰三角形(不含等边三角形)的个数有( ) 已知A、B、C、D四点如图所示,请按如图的要求作图
已知A、B、C、D四点如图所示,请按如图的要求作图 如图,在△ABC中,AB=AC,AB的垂直平分线DG交AC于点G,若AD+AC=24cm,BD+BC=20cm,求△BGC的周长.
如图,在△ABC中,AB=AC,AB的垂直平分线DG交AC于点G,若AD+AC=24cm,BD+BC=20cm,求△BGC的周长.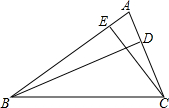 如图,BD、CE是△ABC的高,垂足分别为点D、E.
如图,BD、CE是△ABC的高,垂足分别为点D、E.