题目内容
8. 如图,△ABC为等边三角形,∠ABC的平分线与∠ACB的平分线交于点O,过点O作平行于BC的直线,交AB于M,交AC于N,连接AO,则图中等腰三角形(不含等边三角形)的个数有( )
如图,△ABC为等边三角形,∠ABC的平分线与∠ACB的平分线交于点O,过点O作平行于BC的直线,交AB于M,交AC于N,连接AO,则图中等腰三角形(不含等边三角形)的个数有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
分析 先由已知运用角平分线、平行线的性质以及三角形全等找出相等的角,再根据等角对等边找出等腰三角形.
解答 解:∵△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,
∴∠ABO=∠OBC=∠BCO=∠OCA=30°,
∴△OBC是等腰三角形,
∵MN∥BC,
∴∠BOM=∠OBC=30°,∠NOC=∠BCO=30°,
∴△BOM、△CON是等腰三角形,
在△AOB和△AOC中
$\left\{\begin{array}{l}{AB=AC}\\{OA=OA}\\{OB=OC}\end{array}\right.$
∴△AOB≌△AOC(SSS),
∴∠OAM=∠OAN=30°,
∴△AOB、△AOC是等腰三角形,
所以共有△OBC、△BOM、△CON、△AOB、△AOC,共5个等腰三角形.
故选B.
点评 本题考查了等腰三角形的判定,有两个角相等的三角形是等腰三角形;找出相等的角是解答本题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
18.已知,点A(-2,y1),B(-1,y2),C(1,y3)都在函数y=-2x+b的图象上,则关于y1,y2,y3的大小关系正确的是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y3<y1<y2 |
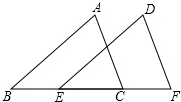 如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.
如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.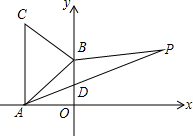 如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内.
如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内. 如图,DE,FG分别是AB,AC的中垂线,若AB=8,AC=5,BC=11,则△ADF的周长=11.
如图,DE,FG分别是AB,AC的中垂线,若AB=8,AC=5,BC=11,则△ADF的周长=11.