题目内容
7.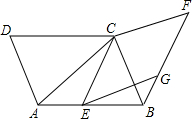 如图,点E是平行四边形ABCD的边AB上的任意一点(不包含端点A,B),分别连接AC,CE,以CE为边作菱形ECFG,再连接BG,已知AB=AC,∠CEG=∠CAB,则下列结论①EG⊥BC,②∠EGB=∠F,③∠CBG=∠CAB,④∠GEB=∠ACE中,一定成立的有②③④(填序号).
如图,点E是平行四边形ABCD的边AB上的任意一点(不包含端点A,B),分别连接AC,CE,以CE为边作菱形ECFG,再连接BG,已知AB=AC,∠CEG=∠CAB,则下列结论①EG⊥BC,②∠EGB=∠F,③∠CBG=∠CAB,④∠GEB=∠ACE中,一定成立的有②③④(填序号).
分析 根据已知条件可以分别证明②③④正确,①可以假设结论成立,推出矛盾即可解决问题.
解答 解:如图,连接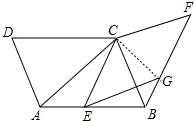 CG.
CG.
∵四边形ECFG是菱形,
∴EC=EG,EG∥CF,
∴∠ECG=∠EGC,∠EGB=∠F,故②正确,
∵AC=AB,
∴∠ACB=∠ABC,
∵∠CEG=∠CAB,
∴∠CEG+2∠ECG=180°,∠BAC+2∠ACB=180°,
∴∠ACB=∠ECG,
∴∠ACE=∠BCG,
∵∠BEC=∠CAB+∠ACE,∠CEG=∠BAC,
∴∠BEG=∠ACE,故④正确,
∵∠BCG=∠ACE=∠BEG,
∴C、G、B、E四点共圆,
∴∠CBG∠CEG=∠CAB,故③正确,
∴∠ECB=∠EGB=∠CEG,
如果EG⊥BC,那么∠ECB=∠CEG=45°,这显然不可能,故①错误.
∴②③④正确.
故答案为②③④.
点评 本题考查菱形的性质、平行四边形的性质、三角形的外角的性质、四点共圆等知识,解题的关键是利用四点共圆的性质,题目比较难,属于中考常考题型.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
17.下列图形中,轴对称图形有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,a∥b,直线c与直线a,b相交,已知∠1=110°,则∠2=70°.
如图,a∥b,直线c与直线a,b相交,已知∠1=110°,则∠2=70°.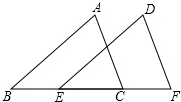 如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.
如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.