题目内容
5. 已知A、B、C、D四点如图所示,请按如图的要求作图
已知A、B、C、D四点如图所示,请按如图的要求作图(1)连接AB
(2)射线CA与射线DB相交于点O
(3)画出一点P,使P到点A、B、C、D的距离之和最小,并说明理由.
分析 (1)直接连接AB即可;
(2)按照作射线的方法即可找出点O;
(3)连接AD、BC,令其交点为P,由三角形的两边之和大于第三边即可得知点P即是所要找的点.
解答 解:(1)连接AB,如图1所示.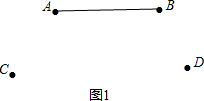
(2)连接CA、DB,延长线段CA,延长线段DB,使二者的交点为点O,如图2所示.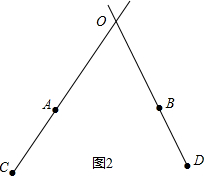
(3)连接AD、BC,令其交点为P,在线段BC上任取一点Q(不同于点P),连接AQ、DQ,如图3所示.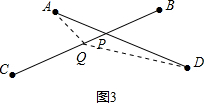
∵点P,点Q均在线段BC上,
∴PB+PC=QB+QC,
∵点P在线段AD上,
∴PA+PD=AD,
在△QAD中,QA+QD>AD(两边之和大于第三部),
即QA+QB+QC+QD>PA+PB+PC+PD.
∴线段AD、BC的交点P为所要找的点.
点评 本题考查了直线、射线和线段,解题的关键是按照画线段、射线和直线的方法完成图形.本题属于基础题,难度不大,解决该题型题目时,根据三角形的三边关系确定点P的位置是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,a∥b,直线c与直线a,b相交,已知∠1=110°,则∠2=70°.
如图,a∥b,直线c与直线a,b相交,已知∠1=110°,则∠2=70°.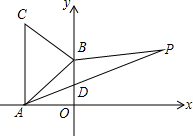 如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内.
如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内.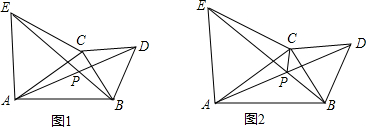
 如图,DE,FG分别是AB,AC的中垂线,若AB=8,AC=5,BC=11,则△ADF的周长=11.
如图,DE,FG分别是AB,AC的中垂线,若AB=8,AC=5,BC=11,则△ADF的周长=11.