题目内容
1．
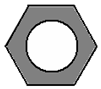如图，六角螺母的横截面是正六边形，它的每条边都相等，每个内角也都相等．求这个六边形的每一个内角的度数．
分析 多边形的内角和可以表示成（n-2）•180°，因为所给多边形的每个内角均相等，可设这个正六边形的每一个内角的度数为x，故又可表示成6x，列方程可求解．
解答 解：设这个正六边形的每一个内角的度数为x，
则6x=（6-2）•180°，
解得：x=120°．
故这个正六边形的每一个内角的度数为120°．
点评 本题考查根据多边形的内角和计算公式求多边形的内角的度数，解答时要会根据公式进行正确运算、变形和数据处理．
练习册系列答案
名校课堂系列答案
相关题目
11．已知：抛物线y=-$\frac{1}{4}$（x+1）2．
（1）写出抛物线的顶点坐标；
（2）完成下表：
（3）在下面的坐标系中描点画出抛物线的图象．
（1）写出抛物线的顶点坐标；
（2）完成下表：
| x | … | -7 | -5 | -3 | -1 | 1 | 3 | 5 | … |
| y | … | -9 | -9 | -1 | 0 | -1 | -4 | -9 | … |
9．已知实数x，y满足|x-4|+$\sqrt{y-8}$=0，则以x，y的值为两边长的等腰三角形的周长为（ ）
| A． | 20或16 | B． | 20 | C． | 16 | D． | 以上答案均不对 |
一块三角形材料如图所示，∠A=30°，∠C=90°，AB=12．用这块材料剪出一个矩形CDEF，其中，点D、E、F分别在BC、AB、AC上（点E与点A、点B均不重合）．设AE=x，矩形CDEF的面积为S．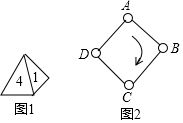
如图1，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字1，2，3，4，如图2，正方形ABCD顶点处各有一个圈，跳圈游戏的规则为：游戏者每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．
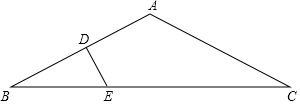如图，△ABC中，AB=AC=2$\sqrt{5}$，BC=8，AB的垂直平分线交AB于点D，交BC于点E，设△BDE的面积为S1，四边形ADEC的面积为S2，则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$．