题目内容
12．若2+$\sqrt{3}$是方程x2-4x+k=0的一个根，则另一根是2-$\sqrt{3}$，k为1．分析 根据一元二次方程根与系数的关系可推另一根是2-$\sqrt{3}$，再由根与系数的关系可求（2$+\sqrt{3}$）（2-$\sqrt{3}$）=k，即k=1．
解答 解：∵方程x2-4x+k=0的一个根是2$+\sqrt{3}$，
设另一根为x，
则x+2+$\sqrt{3}$=4，
解得x=2-$\sqrt{3}$，
∴另一根是2-$\sqrt{3}$，
∵（2$+\sqrt{3}$）（2-$\sqrt{3}$）=k，
∴k=1．
故答案为：2-$\sqrt{3}$；1．
点评 此题主要考查了一元二次方程根与系数的关系，掌握两根之和为$-\frac{b}{a}$，两根之积为$\frac{c}{a}$是解答此题的关键．
练习册系列答案
相关题目
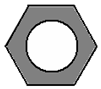如图，六角螺母的横截面是正六边形，它的每条边都相等，每个内角也都相等．求这个六边形的每一个内角的度数．
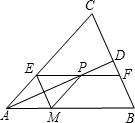如图，等腰△ABC中，AB=AC，AD平分∠BAC交BC于D，在线段AD上任取一点P（点A除外），过点P作EF∥AB，分别交AC、BC于E，F点，作PM∥AC，交AB于M点，连接ME．