题目内容
11．已知：抛物线y=-$\frac{1}{4}$（x+1）2．（1）写出抛物线的顶点坐标；
（2）完成下表：
| x | … | -7 | -5 | -3 | -1 | 1 | 3 | 5 | … |
| y | … | -9 | -9 | -1 | 0 | -1 | -4 | -9 | … |
分析 （1）根据抛物线的解析式即可得到结论；
（2）根据抛物线的解析式填表即可；
（3）根据描点法画出函数的图象即可．
解答 解：（1）由抛物线y=-$\frac{1}{4}$（x+1）2得抛物线的顶点坐标为（-1，0）；
（2）表格填写如下：
| x | … | -7 | -5 | -3 | -1 | 1 | 3 | 5 | … |
| y | … | -9 | -4 | -1 | 0 | -1 | -4 | -9 | … |
点评 本题考查了二次函数的性质，二次函数的图象，正确的作出函数的图象是解题的关键．
练习册系列答案
相关题目
1．要使分式$\frac{x-1}{x+1}$有意义，则x应满足的条件是（ ）
| A． | x≠-1 | B． | x≠1 | C． | x＜-1 | D． | x＞-1 |
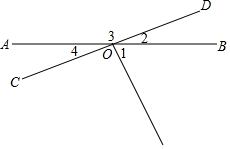如图，直线AB与CD相交于O，∠EOD=90°，填写下列两角关系的名称．
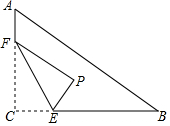如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，且AF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则当点P在线段AB上时，线段PB的长度为$\frac{44}{5}$-4$\sqrt{21}$．
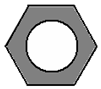如图，六角螺母的横截面是正六边形，它的每条边都相等，每个内角也都相等．求这个六边形的每一个内角的度数．