题目内容
4. 知者加速:
知者加速:(1)如图所示是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁厚度和小圆孔大小忽略不计)范围是12≤a≤13;
(2)观察下列各式,你有什么发现?
32=4+5,52=12+13,72=24+25,92=40+41,…
这到底是巧合,还是有什么规律蕴涵其中呢?请你结合有关知识进行研究.若132=a+b,则a,b的值可能是多少.
分析 (1)构建以5、12为直角边的直角三角形,根据勾股定理即可求出斜边的长度,从而得出a的取值范围;
(2)观察给定等式,根据等式数字的变化找出变化规律“(2n+1)2=(2n2+2n)+(2n2+2n+1)(n为正整数)”,依此规律即可得出结论.
解答 解:(1)构建直角三角形,如图所示.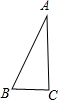
其中AC=12,BC=5,
由勾股定理可得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13.
∴a的取值范围为:12≤a≤13.
故答案为:12≤a≤13.
(2)不是巧合,这些等式中蕴涵着规律.
观察,发现规律:32=4+5,52=12+13,72=24+25,92=40+41,…,
等式的左边=(2n+1)2=4n2+4n+1=(2n2+2n)+(2n2+2n+1)=等式右边,
∴存在规律:(2n+1)2=(2n2+2n)+(2n2+2n+1)(n为正整数).
当n=6时,132=(2×62+2×6)+(2×62+2×6+1)=84+85,
∴a=84,b=85.
点评 本题考查了勾股定理的应用以及规律型中数字的变化类,解题的关键是:(1)根据勾股定理求出斜边的长度;(2)找出变化规律“(2n+1)2=(2n2+2n)+(2n2+2n+1)(n为正整数)”.本题属于基础题,难度不大,解决该题型题目时,根据数字的变化找出变化规律是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.我们知道,在弹性限度内,弹簧挂上重物后会伸长.已知一根弹簧的长度(cm)与所挂重物的质量(kg)之间的关系如下表,则下列说法错误的是( )
| 重物的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
| A. | 在这一变化过程中,重物的质量是自变量,弹簧的长度是因变量 | |
| B. | 当所挂重物的质量是4kg时,弹簧的长度是14cm | |
| C. | 在弹性限度内,当所挂重物的质量是6kg时,弹簧的长度是16cm | |
| D. | 当不挂重物时,弹簧的长度应为12cm |
16.两条对角线互相垂直平分且相等的四边形是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 都有可能 |
13.在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线( )
| A. | 互相垂直 | B. | 相等 | C. | 相交 | D. | 互相平行 |
14.如果电影票上的“5排2号”记作(5,2),那么(4,1)表示( )
| A. | 4排5号 | B. | 5排4号 | C. | 1排4号 | D. | 4排1号 |
 如图,在四边形EBCF中,点A为EF的中点,AB=AC,∠BAC=90°,BE=4$\sqrt{2}$,CF=5$\sqrt{2}$,EF=6,求△ABE的面积.
如图,在四边形EBCF中,点A为EF的中点,AB=AC,∠BAC=90°,BE=4$\sqrt{2}$,CF=5$\sqrt{2}$,EF=6,求△ABE的面积.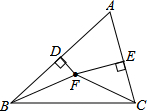 如图所示,已知在△ABC中,AB与AC的垂直平分线分别交AB于点D,交AC于点E,它们相交于点F,求证:BF=FC.
如图所示,已知在△ABC中,AB与AC的垂直平分线分别交AB于点D,交AC于点E,它们相交于点F,求证:BF=FC.