题目内容
14.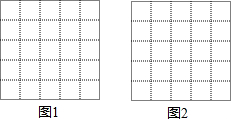 图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.(1)在图1中画出钝角△ABC,使它的面积为6(画一个即可);
(2)在图2中画出△DEF,使它的三边长分别为$\sqrt{5}$、2$\sqrt{5}$、5(画一个即可).并且直接写出此时三角形DEF的面积.
分析 (1)根据三角形的面积公式,画出长3高4的钝角△ABC即可求解;
(2)$\sqrt{5}$的线段是两直角边为1,2的直角三角形的斜边;2$\sqrt{5}$的线段是两直角边为2,4的直角三角形的斜边;依此画出三边长分别为$\sqrt{5}$、2$\sqrt{5}$、5的三角形DEF,再根据三角形的面积公式计算即可求解.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
三角形DEF的面积:$\sqrt{5}$×2$\sqrt{5}$÷2=5
答:三角形DEF的面积是5.
点评 考查了勾股定理,一般应利用构造直角三角形的斜边来求无理数的长度,掌握画图的方法是关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
5.下列说法正确的是( )
| A. | 旋转改变图形的形状和大小 | |
| B. | 平移改变图形的位置 | |
| C. | 图形可以向某方向旋转一定距离 | |
| D. | 由平移得到的图形也一定可由旋转得到 |
2.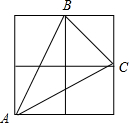 如图,在2×2的网格中,有一个格点三角形△ABC,若每个小正方形的边长为1,则△ABC的边长BC边上的高为( )
如图,在2×2的网格中,有一个格点三角形△ABC,若每个小正方形的边长为1,则△ABC的边长BC边上的高为( )
 如图,在2×2的网格中,有一个格点三角形△ABC,若每个小正方形的边长为1,则△ABC的边长BC边上的高为( )
如图,在2×2的网格中,有一个格点三角形△ABC,若每个小正方形的边长为1,则△ABC的边长BC边上的高为( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | $\frac{3}{2}$$\sqrt{2}$ | D. | 2 |
9.下列方程中,没有实数根的方程是( )
| A. | x2+2x-1=0 | B. | x2+2x+1=0 | C. | x2-x+2=0 | D. | x2-x-2=0 |
6.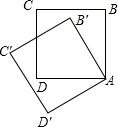 如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )
如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )
 如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )
如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
4.已知∠A=60°,则∠A的补角是( )
| A. | 160° | B. | 120° | C. | 60° | D. | 30° |
 如图所示,已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,夹这个角的两边分别为2a和a(保留作图痕迹,不写作法)
如图所示,已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,夹这个角的两边分别为2a和a(保留作图痕迹,不写作法)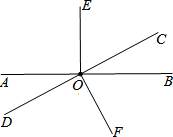 已知,如图直线AB与CD相交于点O,OE⊥AB,过点O作射线OF,∠AOD=30°,∠FOB=∠EOC.
已知,如图直线AB与CD相交于点O,OE⊥AB,过点O作射线OF,∠AOD=30°,∠FOB=∠EOC.