题目内容
3.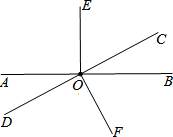 已知,如图直线AB与CD相交于点O,OE⊥AB,过点O作射线OF,∠AOD=30°,∠FOB=∠EOC.
已知,如图直线AB与CD相交于点O,OE⊥AB,过点O作射线OF,∠AOD=30°,∠FOB=∠EOC.(1)求∠EOC度数;
(2)求∠DOF的度数;
(3)直接写出图中所有与∠AOD互补的角.
分析 (1)根据垂直的定义得到∠BOE=90°,由对顶角的性质得到∠BOC=∠AOD=30°,即可得到结论;
(2)根据平角的定义即可得到结论;
(3)根据补角的定义即可得到结论.
解答 解:(1)∵OE⊥AB,
∴∠BOE=90°,
∵∠BOC=∠AOD=30°,
∴∠EOC=60°;
(2)∵∠FOB=∠EOC=60°,
∴∠DOF=180°-∠AOD-∠BOF=90°;
(3)∵∠AOD+∠BOD=180°,
∠AOD+∠AOC=180°,
∠AOD+∠EOF=180°,
∴与∠AOD互补的角是∠AOC;∠BOD;∠EOF.
点评 本题考查了对顶角、邻补角以及角平分线的性质,主要利用对顶角相等,邻补角的定义和角平分线的定义求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.将△ABC的三个顶点的横坐标都加上6,纵坐标都减去5,则所得图形与原图形的关系是( )
| A. | 将原图形向x轴的正方向平移了6个单位,向y轴的正方向平移了5个单位 | |
| B. | 将原图形向x轴的负方向平移了6个单位,向y轴的正方向平移了5个单位 | |
| C. | 将原图形向x轴的负方向平移了6个单位,向y轴的负方向平移了5个单位 | |
| D. | 将原图形向x轴的正方向平移了6个单位,向y轴的负方向平移了5个单位 |
11.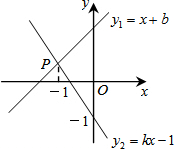 如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )
如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )
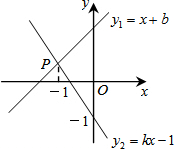 如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )
如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )| A. | x≥-1 | B. | x>-1 | C. | x≤-1 | D. | x<-1 |
18.下列选项是无理数的为( )
| A. | -$\frac{1}{3}$ | B. | $\sqrt{4}$ | C. | 3.1415926 | D. | -π |
15.已知∠1=20°,则∠1的余角度数是( )
| A. | 70° | B. | 80° | C. | 150° | D. | 160° |
12.下列命题中,真命题是( )
| A. | 两条对角线相等的平行四边形是矩形 | |
| B. | 两条对角线相等的四边形是矩形 | |
| C. | 对角线垂直且相等的四边形是正方形 | |
| D. | 两条对角线垂直的四边形是菱形 |
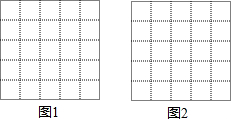 图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形. 将一幅三角板如图放置,若AE∥BC,则∠AFD=75度.
将一幅三角板如图放置,若AE∥BC,则∠AFD=75度.