题目内容
2.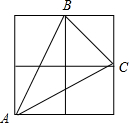 如图,在2×2的网格中,有一个格点三角形△ABC,若每个小正方形的边长为1,则△ABC的边长BC边上的高为( )
如图,在2×2的网格中,有一个格点三角形△ABC,若每个小正方形的边长为1,则△ABC的边长BC边上的高为( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | $\frac{3}{2}$$\sqrt{2}$ | D. | 2 |
分析 首先用大正方形面积减去三个三角形的面积,求出△ABC的面积,再根据勾股定理求得BC边的长度;再根据面积法来求△ABC中BC边上的高.
解答 解:△ABC的面积:
2×2-2×1÷2×2-1×1÷2
=4-2-0.5
=1.5,
BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
△ABC的边长BC边上的高:1.5×2÷$\sqrt{2}$=$\frac{3}{2}\sqrt{2}$.
故选:C.
点评 本题考查了勾股定理,三角形面积的计算.勾股定理应用的前提条件是在直角三角形中.

练习册系列答案
相关题目
13.将△ABC的三个顶点的横坐标都加上6,纵坐标都减去5,则所得图形与原图形的关系是( )
| A. | 将原图形向x轴的正方向平移了6个单位,向y轴的正方向平移了5个单位 | |
| B. | 将原图形向x轴的负方向平移了6个单位,向y轴的正方向平移了5个单位 | |
| C. | 将原图形向x轴的负方向平移了6个单位,向y轴的负方向平移了5个单位 | |
| D. | 将原图形向x轴的正方向平移了6个单位,向y轴的负方向平移了5个单位 |
10.下列说法错误的是( )
| A. | “购买一张福利彩票中奖了”是随机事件 | |
| B. | 调查一批新型节能灯泡的使用寿命适合采用抽样调查 | |
| C. | 在对n个数据进行整理的频数直方图中,各组的频数之和等于n | |
| D. | 一组数据1,2,x,0,-1的极差为4,则x的值是-2 |
17.下列各运算中,计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 2a+3b=5ab | C. | (-3ab2)2=9a2b4 | D. | (a-b)2=a2-b2 |
11.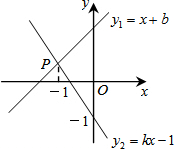 如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )
如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )
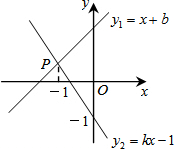 如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )
如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )| A. | x≥-1 | B. | x>-1 | C. | x≤-1 | D. | x<-1 |
12.下列命题中,真命题是( )
| A. | 两条对角线相等的平行四边形是矩形 | |
| B. | 两条对角线相等的四边形是矩形 | |
| C. | 对角线垂直且相等的四边形是正方形 | |
| D. | 两条对角线垂直的四边形是菱形 |




 图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.