题目内容
1.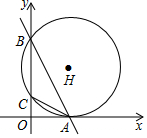 如图,直线y=-2x+8分别交x、y轴于点A、B,点C是线段OB上一点(不与点B重合),过点A、B、C作⊙H,恰好与x轴相切,则∠CAB的正弦值为( )
如图,直线y=-2x+8分别交x、y轴于点A、B,点C是线段OB上一点(不与点B重合),过点A、B、C作⊙H,恰好与x轴相切,则∠CAB的正弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
分析 如图,连接BH、CH、AH,作HE⊥BC于E.由OA是切线,推出OA2=OC•OB,由题意A(4,0),B(0,8),推出OA=4,OB=8,推出OC=2,BC=6,由EH⊥BC,推出BE=EC=3,易证四边形AOEH是矩形,推出EH=OA=4,在Rt△EHB中,BH=$\sqrt{{3}^{2}+{4}^{2}}$=5,再证明∠CAB=∠BHE,即可解决问题.
解答 解:如图,连接BH、CH、AH,作HE⊥BC于E.
∵OA是切线,
∴OA2=OC•OB,
由题意A(4,0),B(0,8),
∴OA=4,OB=8,
∴OC=2,BC=6,
∵EH⊥BC,
∴BE=EC=3,
易证四边形AOEH是矩形,
∴EH=OA=4,
在Rt△EHB中,BH=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵HB=HC,HE⊥BC,
∴∠BHE=∠CHE,
∵∠CAB=$\frac{1}{2}$∠BHC,
∴∠CAB=∠BHE,
∴sin∠CAB=sin∠BHE=$\frac{BE}{BH}$=$\frac{3}{5}$,
故选B.
点评 本题考查解直角三角形、切线的性质、垂径定理、圆周角定理、勾股定理等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.若关于x的分式方程$\frac{2}{x-3}$+$\frac{x+m}{3-x}$=2-$\frac{2}{x-3}$有增根,则m的值是( )
| A. | m=1 | B. | m=0 | C. | m=3 | D. | m=0或m=3 |
6.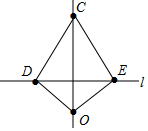 如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
 如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )| A. | 到一个角两边距离相等的点在这个角的角平分线上 | |
| B. | 角平分线上的点到这个角两边的距离相等 | |
| C. | 到线段两端距离相等的点在这条线段的垂直平分线上 | |
| D. | 线段垂直平分线上的点到线段两端的距离相等 |
13. 如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
 如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )| A. | $\frac{π}{2}$-1 | B. | 2π-2 | C. | π+1 | D. | 2π-4 |
10.某林业部门统计某种树苗在本地区一定条件下的移植成活率,结果如表:
根据表中的数据,估计这种树苗移植成活的概率为0.9(精确到0.1);
如果该地区计划成活4.5万棵幼树,那么需要移植这种幼树大约5万棵.
| 移植的棵数n | 300 | 700 | 1000 | 5000 | 15000 |
| 成活的棵数m | 280 | 622 | 912 | 4475 | 13545 |
| 成活的频率$\frac{m}{n}$ | 0.933 | 0.889 | 0.912 | 0.895 | 0.903 |
如果该地区计划成活4.5万棵幼树,那么需要移植这种幼树大约5万棵.
 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.