题目内容
10．某林业部门统计某种树苗在本地区一定条件下的移植成活率，结果如表：| 移植的棵数n | 300 | 700 | 1000 | 5000 | 15000 |
| 成活的棵数m | 280 | 622 | 912 | 4475 | 13545 |
| 成活的频率$\frac{m}{n}$ | 0.933 | 0.889 | 0.912 | 0.895 | 0.903 |
如果该地区计划成活4.5万棵幼树，那么需要移植这种幼树大约5万棵．
分析 利用表格中数据估算这种幼树移植成活率的概率即可．然后用样本概率估计总体概率即可确定答案．
解答 解：由表格数据可得，随着样本数量不等增加，这种幼树移植成活率稳定的0.9左右，
故这种幼树移植成活率的概率约为0.9．
∵该地区计划成活4.5万棵幼树，
∴那么需要移植这种幼树大约4.5÷0.9=5万棵
故本题答案为：0.9；5．
点评 此题主要考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：频率=所求情况数与总情况数之比．
练习册系列答案
相关题目
1．
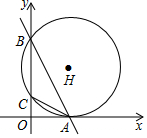如图，直线y=-2x+8分别交x、y轴于点A、B，点C是线段OB上一点（不与点B重合），过点A、B、C作⊙H，恰好与x轴相切，则∠CAB的正弦值为（ ）
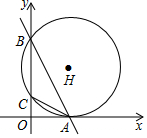如图，直线y=-2x+8分别交x、y轴于点A、B，点C是线段OB上一点（不与点B重合），过点A、B、C作⊙H，恰好与x轴相切，则∠CAB的正弦值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{5}$ |
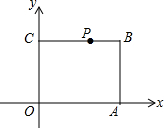在平面直角坐标系中，点A的坐标为（5，0），点C的坐标为（0，4），四边形ABCO为矩形，点P为线段BC上的一动点，若△POA为等腰三角形，且点P在双曲线y=$\frac{k}{x}$上，则k值可以是10或12或8．
20．
在平面直角坐标系中，O为原点，点A（-3，0），点B（0，3），点E、点F分别为OA，OB的中点，若正方形OEDF绕点O顺时针旋转，得到正方形OE′D′F′，若直线AE′与直线BF′相交于点P，则点P的纵坐标的最大值是（ ）
在平面直角坐标系中，O为原点，点A（-3，0），点B（0，3），点E、点F分别为OA，OB的中点，若正方形OEDF绕点O顺时针旋转，得到正方形OE′D′F′，若直线AE′与直线BF′相交于点P，则点P的纵坐标的最大值是（ ）| A． | $\frac{\sqrt{3}+1}{2}$ | B． | $\frac{\sqrt{3}+3}{2}$ | C． | $\frac{\sqrt{3}+3}{4}$ | D． | $\frac{3\sqrt{3}+3}{4}$ |