题目内容
18.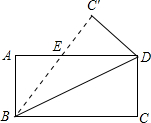 如图,将长方形纸片ABCD沿对角线BD折叠,使点C落在C′处,BC′交AD于E.若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有( )
如图,将长方形纸片ABCD沿对角线BD折叠,使点C落在C′处,BC′交AD于E.若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
分析 根据折叠可得△BCD≌△BC′D,进而可得∠C′BD=∠CBD=22.5°,然后可算出∠C′BC=45°,再根据矩形的性质可得AD∥BC,∠A=∠C′=∠C=90°,然后可得∠AEB=45°,∠ABE=45°,∠EDC′=45°,∠C′ED=45°,从而可得答案.
解答 解:根据折叠可得△BCD≌△BC′D,
∴∠C′BD=∠CBD=22.5°,
∴∠C′BC=45°,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=∠C′=∠C=90°,
∴∠AEB=∠EBC=45°,
∴∠C′ED=45°,
∵∠A=∠C′=∠C=90°,
∴∠ABE=45°,∠EDC′=45°,
∴图中45°的角有5个.
故选:C.
点评 此题主要考查了翻折变换的性质以及矩形的性质,关键是掌握折叠后图形的大小不发生改变.

练习册系列答案
相关题目
9.|1-$\sqrt{2}$|的相反数为( )
| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 1+$\sqrt{2}$ | D. | -1-$\sqrt{2}$ |
13. 如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
 如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )| A. | 2.4cm | B. | 4.8cm | C. | 5cm | D. | 9.6cm |
8.从青岛到济南有南线和北线两条高速公路,南线全长400千米,北线全长320千米.甲、乙两辆客车分别有南线和北线从青岛同时驶往济南,已知客车甲在南线高速公路上行驶的平均速度比客车乙在北线高速公路上快20千米/小时,两车恰好同时到达济南.若设客车乙从青岛到济南的平均速度是x千米/小时,则根据题意可得方程( )
| A. | $\frac{400}{x-20}$=$\frac{320}{x}$ | B. | $\frac{400}{x+20}$=$\frac{320}{x}$ | C. | $\frac{400}{x}$+20=$\frac{320}{x}$ | D. | $\frac{400}{x}$=$\frac{320}{x+20}$ |
