题目内容
3. 已知,如图,在△ABC中,CA=CB,AE、BD分别平分∠CAB和∠CBA,交CB、CA于点E、D,EF、DG分别平分∠CED和∠CDE,交CB、CA于点G、F,BD与AE交于点M,EF与DG交于点N,求证:四边形DMEN是菱形.
已知,如图,在△ABC中,CA=CB,AE、BD分别平分∠CAB和∠CBA,交CB、CA于点E、D,EF、DG分别平分∠CED和∠CDE,交CB、CA于点G、F,BD与AE交于点M,EF与DG交于点N,求证:四边形DMEN是菱形.
分析 先证明△ABD≌△BAE,得出AD=BE,BD=AE,得出DM=EM,CD=CE,得出∠CDE=∠CED,由三角形内角和定理得出∠CAB=∠CBA=∠CDE=∠CED,由角平分线的定义得出∠CDG=∠CEF=∠DAE=∠EBD,得出DG∥AE,EF∥BD,证出四边形DMEN是平行四边形,再由DM=EM,即可得出四边形DMEN是菱形.
解答 证明:∵CA=CB,
∴∠CAB=∠CBA,
∵AE、BD分别平分∠CAB和∠CBA,
∴∠DAE=∠BAE=∠EBD=∠ABD=$\frac{1}{2}$∠CAB=$\frac{1}{2}$∠CBA,
∴AM=BM,
在△ABD和△BAE中,
$\left\{\begin{array}{l}{∠BAD=∠ABE}&{\;}\\{AB=BA}&{\;}\\{∠ABD=∠BAE}&{\;}\end{array}\right.$,
∴△ABD≌△BAE(ASA),
∴AD=BE,BD=AE,
∴DM=EM,CD=CE,
∴∠CDE=∠CED,
∵∠CAB+∠CBA+∠C=180°,∠CDE+∠CED+∠C=180°,
∴∠CAB=∠CBA=∠CDE=∠CED,
∵EF、DG分别平分∠CED和∠CDE,
∴∠CDG=∠CEF=$\frac{1}{2}$∠CDE=$\frac{1}{2}$∠CED,
∴∠CDG=∠CEF=∠DAE=∠EBD,
∴DG∥AE,EF∥BD,
∴四边形DMEN是平行四边形,
又∵DM=EM,
∴四边形DMEN是菱形.
点评 本题考查了等腰三角形的性质与判定、全等三角形的判定与性质、平行四边形的判定方法、菱形的判定方法;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
8.已知A(-1,1)、B(2,-3),若要在x轴上找一点P,使AP+BP最短,此时点P的坐标为( )
| A. | (0,0) | B. | ($\frac{5}{2}$,0) | C. | (-1,0) | D. | (-$\frac{1}{4}$,0) |
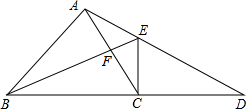 如图所示,在△ABC中,AB=AC,BC的延长线上有一点D,CD=BC,CE⊥BD于点C,交AD于点E,BE交AC于点F.
如图所示,在△ABC中,AB=AC,BC的延长线上有一点D,CD=BC,CE⊥BD于点C,交AD于点E,BE交AC于点F.