题目内容
15.已知[x]表示不大于x的最大的正整数,若a=1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{2009}}$,求[$\sqrt{a}$].分析 根据数的大小比较可得2($\sqrt{k+1}$-$\sqrt{k}$)=$\frac{2}{\sqrt{k+1}+\sqrt{k}}$<$\frac{1}{\sqrt{k}}$<$\frac{2}{\sqrt{k}+\sqrt{k-1}}$=2($\sqrt{k}$-$\sqrt{k-1}$),依此将a变形可求a的范围,再根据[x]表示不大于x的最大的正整数,由二次根式的定义求解.
解答 解:∵2($\sqrt{k+1}$-$\sqrt{k}$)=$\frac{2}{\sqrt{k+1}+\sqrt{k}}$<$\frac{1}{\sqrt{k}}$<$\frac{2}{\sqrt{k}+\sqrt{k-1}}$=2($\sqrt{k}$-$\sqrt{k-1}$),
∴a<1+2($\sqrt{2}$-1)+2($\sqrt{3}$-$\sqrt{2}$)+…+2($\sqrt{2009}$-$\sqrt{2008}$)
=1+2($\sqrt{2009}$-1)
=2$\sqrt{2009}$-1
≈89.64-1
=88.64;
a>2($\sqrt{2}$-1)+2($\sqrt{3}$-$\sqrt{2}$)+…+2($\sqrt{2010}$-$\sqrt{2009}$)
=2($\sqrt{2010}$-1)
=2$\sqrt{2010}$-2
≈89.67-2
=87.67;
∴87.67<a<88.64,
∴9.36<$\sqrt{a}$<9.41,
∴[$\sqrt{a}$]=9.
点评 考查了估算无理数的大小,本题关键是熟悉2($\sqrt{k+1}$-$\sqrt{k}$)=$\frac{2}{\sqrt{k+1}+\sqrt{k}}$<$\frac{1}{\sqrt{k}}$<$\frac{2}{\sqrt{k}+\sqrt{k-1}}$=2($\sqrt{k}$-$\sqrt{k-1}$)的知识点.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案| 每月各户用水量 | 价格(元/吨) |
| 不超过5吨部分 | 3 |
| 超过5吨部分 | 4 |

 已知,如图,在△ABC中,CA=CB,AE、BD分别平分∠CAB和∠CBA,交CB、CA于点E、D,EF、DG分别平分∠CED和∠CDE,交CB、CA于点G、F,BD与AE交于点M,EF与DG交于点N,求证:四边形DMEN是菱形.
已知,如图,在△ABC中,CA=CB,AE、BD分别平分∠CAB和∠CBA,交CB、CA于点E、D,EF、DG分别平分∠CED和∠CDE,交CB、CA于点G、F,BD与AE交于点M,EF与DG交于点N,求证:四边形DMEN是菱形.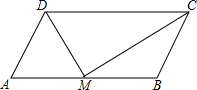 已知:如图,在?ABCD中,AB=2AD,M为AB的中点,连接DM,MC.求证:DM⊥MC.
已知:如图,在?ABCD中,AB=2AD,M为AB的中点,连接DM,MC.求证:DM⊥MC.