题目内容
20.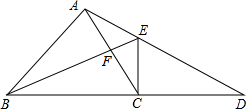 如图所示,在△ABC中,AB=AC,BC的延长线上有一点D,CD=BC,CE⊥BD于点C,交AD于点E,BE交AC于点F.
如图所示,在△ABC中,AB=AC,BC的延长线上有一点D,CD=BC,CE⊥BD于点C,交AD于点E,BE交AC于点F.证明:(1)△BCF∽△DBA;
(2)AF=CF.
分析 (1)首先利用等边对等角得出∠ABC=∠ACB,再利用线段垂直平分线的性质得出BE=DE,进而得出△BCF∽△DBA;
(2)由△BCF∽△DBA,得到$\frac{BC}{CD}=\frac{CF}{AB}$,由于BC=$\frac{1}{2}$CD,于是得到$\frac{CF}{AB}=\frac{1}{2}$,求得CF=$\frac{1}{2}$AC,即可得到结论.
解答 证明:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵BC=CD,EC⊥BD,
∴BE=DE,
∴∠EBC=∠D,
∴△BCF∽△DBA;
(2)∵△BCF∽△DBA,
∴$\frac{BC}{CD}=\frac{CF}{AB}$,
∵BC=CD,
∴BC=$\frac{1}{2}$CD,
∴$\frac{CF}{AB}=\frac{1}{2}$,
∴CF=$\frac{1}{2}$AB,
∵AB=AC,
∴CF=$\frac{1}{2}$AC,
∴AF=CF.
点评 此题主要考查了相似三角形的判定和性质,线段垂直平分线的性质,等腰三角形的性质,根据已知得出∠EBC=∠D是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
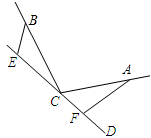 如图,∠BCA=α,CA=CB,C、E、F分别是直线CD上的三点,且∠BEC=∠CFA=α,请提出对EF,BE,AF三条线段之间数量关系的合理猜想,并证明.
如图,∠BCA=α,CA=CB,C、E、F分别是直线CD上的三点,且∠BEC=∠CFA=α,请提出对EF,BE,AF三条线段之间数量关系的合理猜想,并证明. 已知,如图,在△ABC中,CA=CB,AE、BD分别平分∠CAB和∠CBA,交CB、CA于点E、D,EF、DG分别平分∠CED和∠CDE,交CB、CA于点G、F,BD与AE交于点M,EF与DG交于点N,求证:四边形DMEN是菱形.
已知,如图,在△ABC中,CA=CB,AE、BD分别平分∠CAB和∠CBA,交CB、CA于点E、D,EF、DG分别平分∠CED和∠CDE,交CB、CA于点G、F,BD与AE交于点M,EF与DG交于点N,求证:四边形DMEN是菱形.